练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    “ α＝kπ+β(k∈Z)” 是“ tanα＝tanβ” 的

    [　　]

    A. 充分但不必要条件　　  B. 必要但不充分条件

    C. 充分且必要条件　　    D. 既不充分也不必要条件

    　

    答案：B
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：013

    方程sin2x ＝ sin2θ的解集是

    [　　]

    A.｛x│x ＝ kπ+θ,k∈Z｝　　 B.｛x│x ＝ kπ-θ,k∈Z｝

    C.｛x│x ＝ kπ±θ,k∈Z｝　　D.｛x│x ＝ 2kπ+(-1)k·θ,k∈Z｝

    查看答案和解析>>

    科目：高中数学 来源：高二数学 教学与测试 题型：013

    某人用数学归纳法证明＜n＋1(n∈N)的过程如下．

    证 ①当n＝1时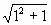，＜1＋1不等式成立；

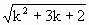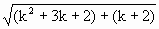    ②假设n＝k(k∈N)时不等式成立，即＜k＋1，那么n＝k＋1时，＝＜＝＝(k＋1)＋1．∴n＝k＋1时，不等式成立，上述证法

    [　　]

    A．过程全部正确　　　　  B．n＝1验证不正确

    C．归纳假设不正确　　    D．从“n＝k到n＝k＋1”的推证不正确

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    某人用数学归纳法证明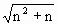＜n＋1(n∈N*)的过程如下．

    证 ①当n＝1时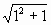，＜1＋1不等式成立；

    　　

    ②假设n＝k(k∈N)时不等式成立，即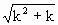＜k＋1，那么n＝k＋1时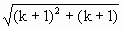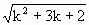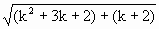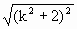，＝＜＝＝(k＋1)＋1．∴n＝k＋1时，不等式成立，上述证法

    [　　]

    A．过程全部正确　　　　  B．n＝1验证不正确

    C．归纳假设不正确　　    D．从“n＝k到n＝k＋1”的推证不正确

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：013

    用数学归纳法证明“当n为正奇数时，xn＋yn能被x＋y整除”，第二步归纳假设应该写成

    [　　]

    A．假设当n＝k(k∈N*)时，xk＋yk能被x＋y整除

    B．假设当n＝2k(k∈N*)时，xk＋yk能被x＋y整除

    C．假设当n＝2k＋1(k∈N*)时，xk＋yk能被x＋y整除

    D．假设当n＝2k－1(k∈N*)时，xk＋yk能被x＋y整除

    查看答案和解析>>

    科目：高中数学 来源：设计选修数学－4-5人教A版 人教A版 题型：013

    用数学归纳法证明“当n为正奇数时，xn＋yn能被x＋y整除”，第二步归纳假设应该写成

    [　　]
    A．

    假设当n＝k(k∈N+)时，xk＋yk能被x＋y整除

    B．

    假设当n＝2k(k∈N+)时，xk＋yk能被x＋y整除

    C．

    假设当n＝2k＋1(k∈N+)时，xk＋yk能被x＋y整除

    D．

    假设当n＝2k－1(k∈N+)时，xk＋yk能被x＋y整除

    查看答案和解析>>

    同步练习册答案