
| A. | $\frac{1}{2π}+\frac{1}{3}$ | B. | $\frac{1}{4π}+\frac{1}{6}$ | C. | $\frac{π}{12}+\frac{1}{4}$ | D. | $\frac{1}{4}+\frac{1}{6π}$ |
分析 联立抛物线和圆的方程求出交点坐标,根据积分的几何意义以及积分的运算法则求出阴影部分的面积,结合几何概型的概率公式进行求解即可.
解答 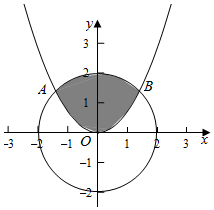 解:将y=$\frac{{\sqrt{2}}}{2}{x^2}$代入x2+y2=4得$\frac{1}{2}$x4+x2=4,即x4+2x2-8=0,得(x2-2)(x2+4)=0,
解:将y=$\frac{{\sqrt{2}}}{2}{x^2}$代入x2+y2=4得$\frac{1}{2}$x4+x2=4,即x4+2x2-8=0,得(x2-2)(x2+4)=0,
得x2-2=0,得x=$\sqrt{2}$或x=-$\sqrt{2}$,此时y=$\frac{\sqrt{2}}{2}×2$=$\sqrt{2}$,即A(-$\sqrt{2}$,$\sqrt{2}$),B($\sqrt{2}$,$\sqrt{2}$),
当y≥0时,由x2+y2=4得y=$\sqrt{4-{x}^{2}}$,
则阴影部分的面积S=∫${\;}_{-\sqrt{2}}^{\sqrt{2}}$($\sqrt{4-{x}^{2}}$-$\frac{{\sqrt{2}}}{2}{x^2}$)dx=∫${\;}_{-\sqrt{2}}^{\sqrt{2}}$$\sqrt{4-{x}^{2}}$dx-∫${\;}_{-\sqrt{2}}^{\sqrt{2}}$$\frac{{\sqrt{2}}}{2}{x^2}$dx,
∫${\;}_{-\sqrt{2}}^{\sqrt{2}}$$\sqrt{4-{x}^{2}}$dx几何意义是x2+y2=4在-$\sqrt{2}$≤x≤$\sqrt{2}$,y≥0时的面积,
则∠AOB=$\frac{π}{2}$,S△AOC=S△BOD=$\frac{1}{2}×\sqrt{2}×\sqrt{2}$=1,
扇形的面积S=$\frac{1}{4}$π×22=π,则∫${\;}_{-\sqrt{2}}^{\sqrt{2}}$$\sqrt{4-{x}^{2}}$dx=1+1+π=2+π,
∫${\;}_{-\sqrt{2}}^{\sqrt{2}}$$\frac{{\sqrt{2}}}{2}{x^2}$dx=$\frac{\sqrt{2}}{2}$×$\frac{1}{3}$x3|${\;}_{-\sqrt{2}}^{\sqrt{2}}$=$\frac{\sqrt{2}}{6}$(($\sqrt{2}$)3-(-$\sqrt{2}$)3)=$\frac{\sqrt{2}}{6}$×4$\sqrt{2}$=$\frac{4}{3}$,
则Ω的面积S=2+π-$\frac{4}{3}$=π+$\frac{2}{3}$,
则在圆O中任取一点P,则P点取自区域Ω中的概率P=$\frac{π+\frac{2}{3}}{π×{2}^{2}}=\frac{π+\frac{2}{3}}{4π}$=$\frac{1}{4}+\frac{1}{6π}$,
故选:D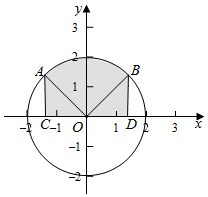
点评 本题主要考查几何概型的概率的计算,根据积分的几何意义和应用求出阴影部分的面积是解决本题的关键.综合性较强,运算量较大,有一定的难度.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$-$\frac{1}{2}$i | B. | $\frac{3}{2}$+$\frac{1}{2}$i | C. | 1+$\frac{1}{2}$i | D. | 1-$\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -sin3°+cos3° | B. | -sin3°+3cos3° | C. | sin3°-cos3° | D. | -sin3°-3cos3° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平均说来甲队比乙队防守技术好 | |
| B. | 甲队比乙队技术水平更稳定 | |
| C. | 甲队有时表现比较差,有时表现又比较好 | |
| D. | 乙队很少不失球 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 游戏1 | 游戏2 |
| 2个红球和2个白球 | 3个红球和1个白球 |
| 取1个球,再取1个球 | 取1个球,再取1个球 |
| 取出的两个球同色→甲胜 | 取出的两个球同色→甲胜 |
| 取出的两个球不同色→乙胜 | 取出的两个球不同色→乙胜 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
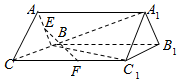 如图,三棱柱ABC-A1B1C1中,CC1=BC1=$\sqrt{2}$,BC=2,△ABC是以BC为底边的等腰三角形,平面ABC⊥平面BCC1B1,E、F分别为棱AB、CC1的中点.
如图,三棱柱ABC-A1B1C1中,CC1=BC1=$\sqrt{2}$,BC=2,△ABC是以BC为底边的等腰三角形,平面ABC⊥平面BCC1B1,E、F分别为棱AB、CC1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com