解:(Ⅰ)因为向量

=(a,cosB),

=(b,cosA)且

,
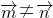
,所以,acosA=sinB.--------(1分)
由正弦定理,可得sinAcosA=sinBcosB,即 sin2A=sin2B.--------------(2分)
所以 2A+2B=π,即 A+B=

.-------(3分)
再由sinA+sinB=

,以及sinA+sinB=sinA+cosA=

sin(A+

),可得
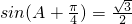
.------(4分)
由于 A为锐角,故有A+

=

或A+

=

,∴
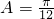
,或

.------(6分)
(Ⅱ)若△ABC的外接圆半径为1,且abx=a+b,则 x=

,由正弦定理,得
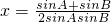
.-----(8分)
设 sinA+cosA=t,t∈(1,

),则 t
2=1+2sinAcosA,∴sinAcosA=

,-----------(10分)
即
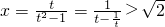
,所以实数x的取值范围为
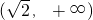
.---------(12分)
分析:(Ⅰ)由两个向量共线的性质求得sin2A=sin2B,故A+B=

.再由sinA+sinB=

,求得
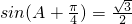
,可得A+

=

或A+

=

,由此求得A的值.
(Ⅱ)由条件结合正弦定理可得
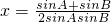
,设 sinA+cosA=t,t∈(1,

),根据
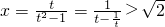
,求得实数x的取值范围.
点评:本题主要考查两个向量共线的性质,正弦定理两角和差的正弦公式的应用,属于中档题.

 =(a,cosB),
=(a,cosB), =(b,cosA)且
=(b,cosA)且 ,
,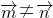
 ,求A;
,求A; =(a,cosB),
=(a,cosB), =(b,cosA)且
=(b,cosA)且 ,
,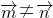 ,所以,acosA=sinB.--------(1分)
,所以,acosA=sinB.--------(1分) .-------(3分)
.-------(3分) ,以及sinA+sinB=sinA+cosA=
,以及sinA+sinB=sinA+cosA= sin(A+
sin(A+ ),可得
),可得 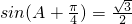 .------(4分)
.------(4分) =
= 或A+
或A+ =
= ,∴
,∴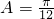 ,或
,或 .------(6分)
.------(6分) ,由正弦定理,得
,由正弦定理,得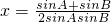 .-----(8分)
.-----(8分) ),则 t2=1+2sinAcosA,∴sinAcosA=
),则 t2=1+2sinAcosA,∴sinAcosA= ,-----------(10分)
,-----------(10分)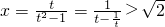 ,所以实数x的取值范围为
,所以实数x的取值范围为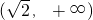 .---------(12分)
.---------(12分) .再由sinA+sinB=
.再由sinA+sinB= ,求得
,求得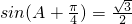 ,可得A+
,可得A+ =
= 或A+
或A+ =
= ,由此求得A的值.
,由此求得A的值.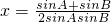 ,设 sinA+cosA=t,t∈(1,
,设 sinA+cosA=t,t∈(1, ),根据
),根据 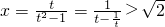 ,求得实数x的取值范围.
,求得实数x的取值范围.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案