Question

三次函数f(x)=x³+bx²+cx+d的图像大致如图所示，图中的实数t满足≤t＜1．

(1)试求c、d的值(或用t表示)．

(2)试用t表示f(x)在区间[1，2]上的最值；

(3)若不等式t²-mt＞f(x)在x∈[1，2]时恒成立，求实数m的取值范围．

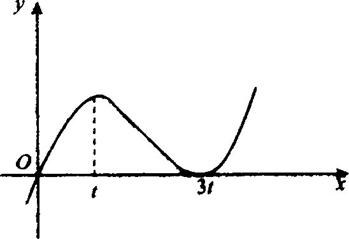
第21题图

Answer 1

答案：(1)f′(x)=3x²+2bx+c．

第21题图

由图知，t与3t是函数f(x)的极值点．∴t与3t是方程3x²+2bx+c=0的两根．

于是，t+3t=b=-6t；t·3t=c=9t²；

f(0)=0d=0．

(2)f(x)=x³-6tx²+9t²x.

∵≤t≤1[1，2][t，3t]．

∴f(x)在[1，2]上递减．

于是，f(x)_max=f(1)=1-6t+9t²；f(x)_min=f(2)=8-24t+36t²．

(3)“t²-mt＞f(x)在x∈[1，2]时恒成立”等价于t-mt＞f(x)max=1-6t+9t²．

∵t＞0，∴m＜6-(8t+)．

令φ(t)=6-(8t+)(≤t≤1)．

则φ(t₁)-φ(t₂)=[6-(8t₁+)]-[6-(8t₂+)]=(t₁-t₂)(-8)

设≤t₁＜t₂≤1，则t₁-t₂＜0，-8＜0．

∴φ(t₁)＞φ(t₂)φ(t)在[，1]上递减．

从而φ(t)_min=φ()=6．

故m＜.