
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| A1 |
| 1 |
| 4 |
| A2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 16 |
| A3 |
| 3 |
| 4 |
| 1 |
| 4 |
| 9 |
| 64 |
| A4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 27 |
| 256 |
| 3 |
| 4 |
| 81 |
| 256 |
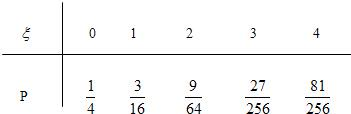
| 1 |
| 4 |
| 3 |
| 16 |
| 9 |
| 64 |
| 27 |
| 256 |
| 81 |
| 256 |
| 525 |
| 256 |
| 81 |
| 256 |
| 175 |
| 256 |
| 175 |
| 256 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
(04年重庆卷理)(12分)
设一汽车在前进途中要经过4个路口,汽车在每个路口遇到绿灯的概率为![]() ,遇到红灯(禁止通行)的概率为
,遇到红灯(禁止通行)的概率为![]()
![]() 假定汽车只在遇到红灯或到达目的地才停止前进,
假定汽车只在遇到红灯或到达目的地才停止前进,![]() 表示停车时已经通过的路口数,求:
表示停车时已经通过的路口数,求:
(1)![]() 的概率的分布列及期望E
的概率的分布列及期望E![]() ;
;
(2 ) 停车时最多已通过3个路口的概率![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)ξ的概率的分布列及期望Eξ;
(2)停车时最多已通过3个路口的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)ξ的概率分布列及期望Eξ;
(2)停车时最多已通过3个路口的概率.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三综合练习一理科数学试卷(解析版) 题型:解答题
设一汽车在前进途中要经过4个路口,汽车在每个路口遇到绿灯的概率为 ,遇到红灯(禁止通行)的概率为
,遇到红灯(禁止通行)的概率为 假定汽车只在遇到红灯或到达目的地才停止前进,
假定汽车只在遇到红灯或到达目的地才停止前进, 表示停车时已经通过的路口数,求:
表示停车时已经通过的路口数,求:
(1) 的概率的分布列及期望E
的概率的分布列及期望E ;
;
(2 ) 停车时最多已通过3个路口的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com