
当![]() >0,
>0,
那么m2-
解:由![]() ;?
;?
由![]() >0,得m<-3或m>
>0,得m<-3或m>![]() .?
.?
又m>-![]() ,得m>
,得m>![]() .?
.?
由m2-
由m>-![]() ,得2<m<3.?
,得2<m<3.?
由此可知,原命题可变为“如果m>![]() ,那么2<m<3.”显然是假命题.?
,那么2<m<3.”显然是假命题.?
逆命题为“当
如果m2-![]() >0.”
>0.”
此命题即是“如果2<m<3,那么m>![]() ”,是真命题.
”,是真命题.
否命题为“当
如果![]() ≤0,
≤0,
那么m2-
因为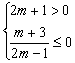
![]()
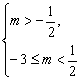 ?
?![]() -
-![]() <m<
<m<![]() ,?
,?
![]()
![]()
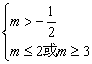
![]() -
-![]() <m≤2或m≥3,?
<m≤2或m≥3,?
则否命题可表述为“如果-![]() <m<
<m<![]() ,那么-
,那么-![]() <m≤2或m≥
<m≤2或m≥
逆否命题为“当
如果m2-![]() ≤0.”
≤0.”
它可表述为“如果-![]() <m≤2或m≥3,
<m≤2或m≥3,
那么-![]() <m<
<m<![]() ”,是假命题.
”,是假命题.
点评:从集合的角度判断命题的真假有:“设A![]() B,若x∈A则x∈B”是真命题,“设A
B,若x∈A则x∈B”是真命题,“设A![]() B,若x∈A则x∈B”是假命题.
B,若x∈A则x∈B”是假命题.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com