
如图,P—ABCD是正四棱锥,ABCD—A1B1C1D1是正方体,其中AB=2,PA= ![]() .
.
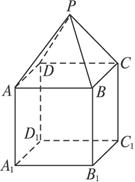
(1)求证:PA⊥B1D1;
(2)求平面PAD与平面BDD1B1所成的锐二面角的大小;
(3)求B1到平面PAD的距离.
解法一:(1)以D1为原点,D1A1为x轴,D1C1为y轴,DD1为z轴建立空间直角坐标系,D1(0,0,0),A1(2,0,0),B1(2,2,0),C1(0,2,0),D(0,0,2),A(2,0,2),B(2,2,2),C(0,2,2),P(1,1,4).
∵![]() =(-1,1,2),
=(-1,1,2),![]() =(2,2,0),
=(2,2,0),
∴![]() ·
·![]() =0,
=0,
即PA⊥D1B1.
(2)平面BDD1B1的法向量为![]() =(-2,2,0),
=(-2,2,0),![]() =(2,0,0),
=(2,0,0),![]() =(1,1,2),
=(1,1,2),
设平面PAD的法向量为n=(x,y,z),则n⊥![]() 且n⊥
且n⊥![]() ,
,
∴![]()
![]() 取n=(0,2,-1),
取n=(0,2,-1),
设所求的锐二面角为θ,则
cosθ=|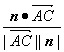 |=
|=![]() ,
,
θ=arccos![]() .
.
(3)![]() =(2,2,-2),设所求的距离为d,
=(2,2,-2),设所求的距离为d,
则d=|![]() |=
|=![]() .
.
解法二:(1)连结AC,交BD于点O,连结PO,则PO⊥平面ABCD.
又∵AC⊥BD,∴PA⊥BD.
∵BD∥B1D1,∴PA⊥B1D1.
(2)∵AO⊥BD,∴AO⊥PO.∴AO⊥平面PBD.
过点O作OM⊥PD于点M,连结AM,则AM⊥PD.
∴∠AMO就是二面角APDO的平面角.
∵AB=2,PA=![]() ,
,
∴AO=![]() ,PO=
,PO=![]() =2,OM=
=2,OM=![]() =
=![]() =
=![]() .
.
∴tan∠AMO=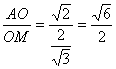 ,
,
即二面角的大小为arctan![]() .
.
(3)用体积法求解:连结B1P,B1D,B1A,
则![]()
![]()
![]() h·S△PAD=
h·S△PAD=![]() AO·
AO·![]() ,
,
即有![]() h·
h·![]() ·2·
·2·![]() =
=![]() ·
·![]() ·
·![]() ·
·![]() ,
,
解得h=![]() ,即B1到平面PAD的距离为
,即B1到平面PAD的距离为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
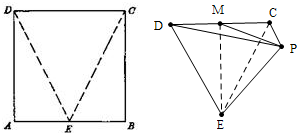 如图,ABCD是正方形,E是AB的中点,如将△DAE和△CBE分别沿虚线DE和CE折起,使AE与BE重合,记A与B重合后的点为P,则面PCD与面ECD所成的二面角为
如图,ABCD是正方形,E是AB的中点,如将△DAE和△CBE分别沿虚线DE和CE折起,使AE与BE重合,记A与B重合后的点为P,则面PCD与面ECD所成的二面角为查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:
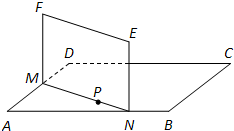 如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD,AB距离分别为9m,3m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF,MN:NE=16:9.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD,AB距离分别为9m,3m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF,MN:NE=16:9.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):
如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com