Question

（04年福建卷文）（12分）

如图，P是抛物线C：y=x²上一点，直线l过点P并与抛物线C在点P的切线垂直，l与抛物线C相交于另一点Q.

（Ⅰ）当点P的横坐标为2时，求直线l的方程；

（Ⅱ）当点P在抛物线C上移动时，求线段PQ中点M的轨迹方程，并求点M到x轴的最短距离.

 

 

 

 

 

 

 

 

Answer 1

解析：（Ⅰ）把x=2代入，得y=2， ∴点P坐标为（2，2）.

由  ，  ①     得，  ∴过点P的切线的斜率=2，

直线l的斜率k_l=－=   ∴直线l的方程为y－2=－(x－2)，

即 x+2y－6=0.

（Ⅱ）设

∵ 过点P的切线斜率 =x₀，当x₀=0时不合题意，

  ∴ 直线l的斜率k_l=－=，

直线l的方程为      ②

方法一：联立①②消去y，得x²+x－x₀²－2=0.   设Q  

∵M是PQ的中点，

∴

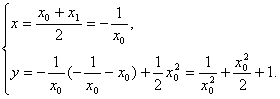
消去x₀，得y=x²+(x≠0)就是所求的轨迹方程.

由x≠0知

上式等号仅当时成立，所以点M到x轴的最短距离是

方法二：

设Q则

由y₀=x₀²，y₁=x₁²，x=

∴ y₀－y₁=x₀²－x₁²=(x₀+x₁)(x₀－x₁)=x(x₀－x₁)，

∴   ∴

将上式代入②并整理，得  y=x²+(x≠0)就是所求的轨迹方程.

由x≠0知

上式等号仅当时成立，所以点M到x轴的最短距离是