
若![]() =
=![]() ,
,![]() =
=![]() ,其中ω>0,记函数f(x)=(
,其中ω>0,记函数f(x)=(![]() +
+![]() )·
)·![]() +k.
+k.
(1)若f(x)图象中相邻两条对称轴间的距离不小于![]() ,求ω的取值范围.
,求ω的取值范围.
(2)若f(x)的最小正周期为π,且当x![]() 时,f(x)的最大值是
时,f(x)的最大值是![]() ,求f(x)的解析式,并说明如何由y=sinx的图象变换得到y=f(x)的图象.
,求f(x)的解析式,并说明如何由y=sinx的图象变换得到y=f(x)的图象.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:浙江省台州市蓬街私立中学2011-2012学年高二下学期第一次月半考数学文科试题 题型:013
给出下面类比推理命题(其中Q为有理数集,R为实数集,C为复数集)
①“若a,b∈R,则a-b=0![]() a=b”类比推出“a,b∈C,则a-b=0
a=b”类比推出“a,b∈C,则a-b=0![]() a=b”
a=b”
②“若a,b,c,d∈R,则复数a+bi=c+di![]() a=c,b=d”类比推出“若a,b,c,d∈Q,则a+b
a=c,b=d”类比推出“若a,b,c,d∈Q,则a+b![]() =c+d
=c+d![]()
![]() a=c,b=d”;
a=c,b=d”;
③若“a,b∈R,则a-b>0![]() a>b”类比推出“a,b∈C,则a-b>0
a>b”类比推出“a,b∈C,则a-b>0![]() a>b”
a>b”
其中类比结论正确的个数是
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省泰安市高三12月质检文科数学试卷(解析版) 题型:解答题
若 =
= ,
, =
= ,其中
,其中 >0,记函数f(x)=2
>0,记函数f(x)=2 ·
· ,f(x)图象中相邻两条对称轴间的距离为
,f(x)图象中相邻两条对称轴间的距离为 ,
,
(1)求 的值;
的值;
(2)求f(x)的单调减区间和f(x)的最大值及取得最大值时x的取值集合.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三第二次月考文科数学卷 题型:解答题
若 =
= ,
, =
= ,其中
,其中 >0,记函数f(x)=2
>0,记函数f(x)=2 ·
· ,f(x)图象中相邻两条对称轴间的距离为
,f(x)图象中相邻两条对称轴间的距离为 ,(1)求
,(1)求 的值;
的值;
(2)求f(x)的单调减区间和f(x)的最大值及取得最大值时x的取值集合.
查看答案和解析>>
科目:高中数学 来源:福建省漳州三中2010-2011学年高三第二次月考数学(文) 题型:解答题
若 =
= ,
, =
= ,其中
,其中 >0,记函数f(x)=2
>0,记函数f(x)=2 ·
· ,f(x)图象中相邻两条对称轴间的距离为
,f(x)图象中相邻两条对称轴间的距离为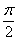 ,(1)求
,(1)求 的值;(2)求f(x)的单调减区间和f(x)的最大值及取得最大值时x的取值集合.
的值;(2)求f(x)的单调减区间和f(x)的最大值及取得最大值时x的取值集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com