
设 是数列
是数列 的前
的前 项和,对任意
项和,对任意 都有
都有 成立, (其中
成立, (其中 、
、 、
、 是常数).
是常数).
(1)当 ,
, ,
, 时,求
时,求 ;
;
(2)当 ,
, ,
, 时,
时,
①若 ,
,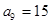 ,求数列
,求数列 的通项公式;
的通项公式;
②设数列 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“ 数列”.
数列”.
如果 ,试问:是否存在数列
,试问:是否存在数列 为“
为“ 数列”,使得对任意
数列”,使得对任意 ,都有
,都有
 ,且
,且 .若存在,求数列
.若存在,求数列 的首项
的首项 的所
的所
有取值构成的集合;若不存在,说明理由.
(1)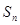 =
=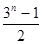 ;(2)①
;(2)①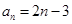 ;②存在,首项
;②存在,首项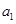 的所有取值构成的集合为
的所有取值构成的集合为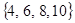 .
.
【解析】
试题分析:(1)要求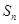 ,大多数时候要先求
,大多数时候要先求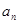 ,本题实质就是有关系式
,本题实质就是有关系式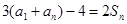 ,那么我们可以用
,那么我们可以用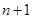 代
代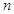 得
得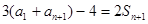 ,两式相减,可得出
,两式相减,可得出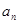 与
与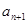 的关系,本题正好得到数列
的关系,本题正好得到数列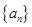 是等比数列,故易求得
是等比数列,故易求得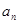 和
和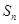 ;(2) 实质上的关系式是
;(2) 实质上的关系式是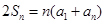 ,这让我们联想到数列
,这让我们联想到数列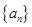 是等差数列,这里难点就在于证明
是等差数列,这里难点就在于证明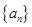 是等差数列,证明方法是把等式
是等差数列,证明方法是把等式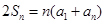 中的
中的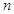 用
用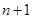 换得到一个式子,两式相减可得
换得到一个式子,两式相减可得 ,此式中含有常数
,此式中含有常数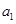 ,故再一次用
,故再一次用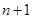 代换此式中的
代换此式中的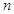 ,两式相减可消去
,两式相减可消去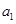 得数列
得数列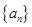 的连续三项
的连续三项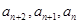 的关系,可证得
的关系,可证得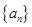 是等差数列,那么这里①的通项公式易求;对于②这类问题总是假设存在,然后去求,假设存在时,可知数列公差是2,即
是等差数列,那么这里①的通项公式易求;对于②这类问题总是假设存在,然后去求,假设存在时,可知数列公差是2,即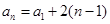 ,由于它是“
,由于它是“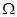 数列”,故任意两项和还是数列中的项,即
数列”,故任意两项和还是数列中的项,即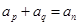 ,可得
,可得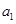 是偶数,又由
是偶数,又由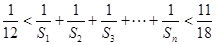 ,得
,得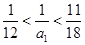 ,娵
,娵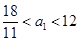 ,从而
,从而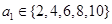 ,下面对
,下面对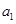 的值一一验证是否符合已知条件
的值一一验证是否符合已知条件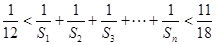 ,
,
试题解析:(1)当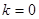 ,
,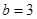 ,
,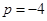 时,由
时,由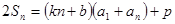 得
得
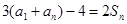 ①
①
用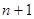 去代
去代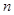 得,
得,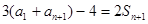 ,
②
,
②
②—①得,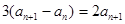 ,
,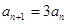 ,
,
在①中令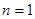 得,
得,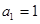 ,则
,则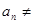 0,∴
0,∴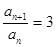 ,
,
∴数列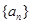 是以首项为1,公比为3的等比数列,
是以首项为1,公比为3的等比数列,
∴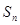 =
=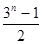
(2)当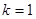 ,
,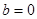 ,
, 时,
时,
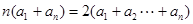 , ③
, ③
用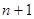 去代
去代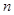 得,
得,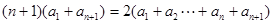 , ④
, ④
④—③得,
 , ⑤
, ⑤
用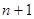 去代
去代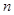 得,
得,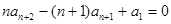 , ⑥
, ⑥
⑥—⑤得,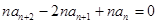 ,即
,即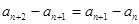 ,
,
∴数列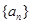 是等差数列.∵
是等差数列.∵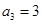 ,
,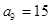 ,
,
∴公差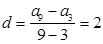 ,∴
,∴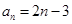
易知数列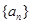 是等差数列,∵
是等差数列,∵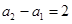 ,∴
,∴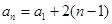 .
.
又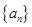 是“
是“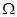 数列”,得:对任意
数列”,得:对任意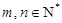 ,必存在
,必存在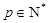 使
使
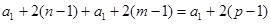 ,
,
得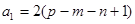 ,故
,故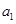 是偶数,
是偶数,
又由已知,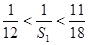 ,故
,故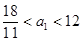
一方面,当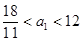 时,
时,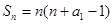
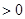 ,对任意
,对任意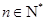 ,
,
都有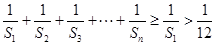
另一方面,当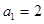 时,
时,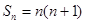 ,
,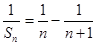 ,
,
则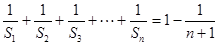 ,
,
取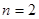 ,则
,则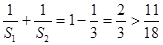 ,不合题意.
,不合题意.
当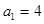 时,
时,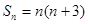 ,
,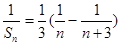 ,则
,则
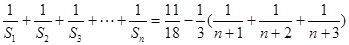
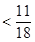 ,
,
当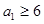 时,
时,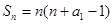
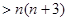 ,
,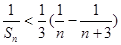 ,
,
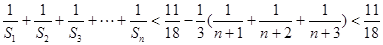 ,
,
又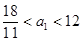 ,∴
,∴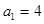 或
或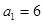 或
或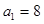 或
或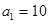
所以,首项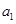 的所有取值构成的集合为
的所有取值构成的集合为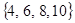
(其他解法,可根据【解】的评分标准给分)
考点:(1)已知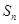 与
与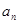 的关系,求
的关系,求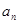 和
和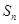 ;(2)等差数列的通项公式,前
;(2)等差数列的通项公式,前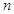 项和
项和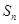 .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
已知函数![]() 满足
满足![]() ,且
,且![]()
(1)当![]() 时,求
时,求![]() 的表达式;
的表达式;
(2)设![]() ,
,![]() ,求证:
,求证:![]() ;w.w.w.k.s.5.u.c.o.m
;w.w.w.k.s.5.u.c.o.m ![]()
(3)设![]() ,对每一个
,对每一个![]() ,在
,在![]() 与
与![]() 之间插入
之间插入![]() 个
个![]() ,得到新数列
,得到新数列![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,试问是否存在正整数
项和,试问是否存在正整数![]() ,使
,使![]() ?若存在求出
?若存在求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)设![]() 为数列
为数列![]() 的前
的前![]() 项和,对任意的
项和,对任意的![]() N
N![]() ,都有
,都有![]()
![]() 为常数,且
为常数,且![]() .(1)求证:数列
.(1)求证:数列![]() 是等比数列;
是等比数列;
(2)设数列![]() 的公比
的公比![]() ,数列
,数列![]() 满足
满足![]()
![]() ,
,![]() N
N![]()
![]() ,求数列
,求数列![]() 的通项公式;(3)在满足(2)的条件下,求证:数列
的通项公式;(3)在满足(2)的条件下,求证:数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源:2014届广东省“十校”高三第一次联考理科数学试卷(解析版) 题型:解答题
设 为数列
为数列 的前
的前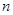 项和,对任意的
项和,对任意的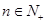 ,都有
,都有 (
(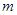 为正常数).
为正常数).
(1)求证:数列 是等比数列;
是等比数列;
(2)数列 满足
满足 求数列
求数列 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列 的前
的前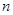 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源:2013届湖北省咸宁赤壁市期中新四校联考高一(理科)数学试卷 题型:解答题
设数列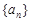 的前
的前 项和为
项和为 ,
,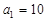 ,
, .
.
⑴求证:数列 是等差数列.
是等差数列.
⑵设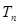 是数列
是数列 的前
的前 项和,求使
项和,求使 对所有的
对所有的 都成立的最大正整数
都成立的最大正整数 的值. (本题满分12分)
的值. (本题满分12分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com