
分析 (1)利用△AF1B的周长为4$\sqrt{3}$,椭圆的离心率为$\frac{\sqrt{6}}{3}$,确定几何量,从而可得椭圆的方程;
(2)设A为弦MN的中点,直线与椭圆方程联立得(3k2+1)x2+6mkx+3(m2-1)=0,由于直线与椭圆有两个交点,可得m2<3k2+1,|PM|=||PN|,可得AP⊥MN,由此可推导出m的取值范围.
解答 解:(1)∵△AF1B的周长为4$\sqrt{3}$,椭圆的离心率为$\frac{\sqrt{6}}{3}$,
∴a=$\sqrt{3}$,c=$\sqrt{2}$
∴b=1,
∴椭圆的方程为:$\frac{{x}^{2}}{3}+{y}^{2}$=1;
(2)设A(xA,yA)、M(xM,yM)、N(xN,yN),A为弦MN的中点,
直线y=kx+m与椭圆方程联立,消去y可得(3k2+1)x2+6mkx+3(m2-1)=0,
∵直线与椭圆相交,∴△=(6mk)2-12(3k2+1)(m2-1)>0,∴m2<3k2+1,①
由韦达定理,可得A(-$\frac{3km}{1+3{k}^{2}}$,$\frac{m}{1+3{k}^{2}}$)
∵|PM|=||PN|,∴AP⊥MN,
∴$\frac{\frac{m}{1+3{k}^{2}}+1}{-\frac{3km}{1+3{k}^{2}}}•k=-1$
∴2m=3k2+1②
把②代入①得2m>m2解得0<m<2
∵2m=3k2+1>1,∴m>$\frac{1}{2}$
∴$\frac{1}{2}$<m<2.
当k=0时,m=$\frac{1}{2}$,也成立.
综上可得m的范围是[$\frac{1}{2}$,2).
点评 本题考查椭圆的方程,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
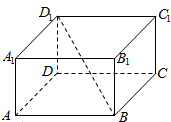 如图,长方体ABCD-A1B1C1D1中,O为BD1的中点,三棱锥O-ABD的体积为V1,四棱锥O-ADD1A1的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为$\frac{1}{2}$.
如图,长方体ABCD-A1B1C1D1中,O为BD1的中点,三棱锥O-ABD的体积为V1,四棱锥O-ADD1A1的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com