练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，在面积为18的△ABC中，AB=5，双曲线E过点A，
     
    且以B、C为焦点，已知

    （Ⅰ）建立适当的坐标系，求双曲线E的方程；

    （Ⅱ）是否存在过点D（1，1）的直线l，

    使l与双曲线E交于不同的两点M、N，且

    如果存在，求出直线l的方程；如果不存在，请说明理由.

    （Ⅰ）（Ⅱ）不存在满足条件的直线l.


    解析:

    （Ⅰ）以BC所在直线为x轴，线段BC的中点O为原点，线段BC的中垂线为y轴建立坐标系如图.  设  2分

        则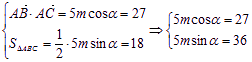  两式平方相加，得m=9.   ………2分

    又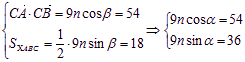两式平方相加，得   2分

    设双曲线的方程为     由双曲线的定义，

    有2a=||AC|－|AB||=|m－5|=4，即a=2.    又2c=，即

    ∴b2=c2－a2=9.     ∴双曲线E的方程为 ……2分

    （Ⅱ）假设存在满足条件的直线l，使l与双曲线E交于不同两点M、N，

    并设  由知点D是线段MN的中点，

    ∴  …………1分    由于点M、N都在双曲线E上，

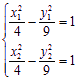    ∴.    将两式相减，得

    此时直线l的方程为  ……3分

    但由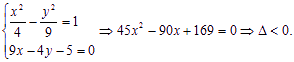∴不存在满足条件的直线l.  …2分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，在面积为18的△ABC中，AB=5，双曲线E过点A，且以B、C为焦点，已知
    AB
    •
    AC
    =27，
    CA
    •
    CB
    =54．
    （1）建立适当坐标系，求双曲线E的方程；
    （2）是否存在过点D（1，1）的直线l，使l与双曲线交于不同的两点M、N，且
    DM
    +
    DN
    =0．如果存在，求出直线l的方程；如果不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：天利38套《2008全国各省市高考模拟试题汇编　精华大字版》、数学理 题型：044

    在面积为18的△ABC中，AB＝5，双曲线E过点A，且以B、C为焦点，已知·＝27，·＝54．如图，以BC所在直线为x轴，BC中点O为原点建立直角坐标系．

    (Ⅰ)求曲线E的方程；

    (Ⅱ)是否存在过点D(1，1)的直线L，使L与双曲线E交于不同的两点M、N，且＋＝0，如果存在，求出L的方程；如果不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在面积为18的△ABC中，AB=5，双曲线E过点A，且以B、C为焦点,已知=27，=54.

    如图，以BC所在直线为x轴，BC中点O为原点建立直角坐标系.

    (Ⅰ)求曲线E的方程；

    (Ⅱ)是否存在过点D(1，1)的直线L，使L与双曲线E交于不同的两点M、N，且=0，如果存在，求出L的方程；如果不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源：2005年广东省深圳市罗湖区高考数学模拟试卷（解析版） 题型：解答题

    如图，在面积为18的△ABC中，AB=5，双曲线E过点A，且以B、C为焦点，已知=27，=54．
    （1）建立适当坐标系，求双曲线E的方程；
    （2）是否存在过点D（1，1）的直线l，使l与双曲线交于不同的两点M、N，且=0．如果存在，求出直线l的方程；如果不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案