练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知复数z1=cosθ-i，z2=sinθ+i，则z1•z2的实部最大值为    ，虚部最大值为    ．
    【答案】分析：把复数z1=cosθ-i，z2=sinθ+i，代入z1•z2化简，求出它的实部最大值，虚部最大值．
    解答：解：z1•z2=（cosθsinθ+1）+i（cosθ-sinθ）．
    实部为cosθsinθ+1=1+sin2θ≤，
    所以实部的最大值为．
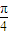
    虚部为cosθ-sinθ=sin（-θ）≤，
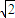
    所以虚部的最大值为．
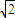
    故答案为：、
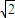    点评：本题考查复数的代数形式的乘除运算，复数的基本概念，三角函数的有关计算，是基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知复数z1=cosθ-i，z2=sinθ+i，则z1•z2的实部最大值为
     
    ，虚部最大值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知复数z1=cosθ-i，z2=sinθ+i，求|z1•z2|的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知复数z1=cosα+isinα，z2=cosβ+isinβ，|z1-z2|=
    2
    5
    		5
    ，求：cos（α-β）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知复数z1=cos
    π
    9
    +isin
    π
    9
    和复数z2=cos
    π
    18
    +isin
    π
    18
    ，则复数z1•z2的实部是
    		3
    2
    		3
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2009•金山区二模）已知复数z1=cosθ+i和z2=1-isinθ，i为虚数单位，求|z1-z2|2的最大值和最小值，并写出相应的θ的取值．

    查看答案和解析>>

    同步练习册答案