练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知不等式，对满足的一切实数都成立，则实数的取值范围为______

    【答案】

    【解析】

    试题不等式|a﹣1|≥x+2y+2z恒成立，只要|a﹣1|≥（x+2y+2z）max，利用柯西不等式9=（12+22+22）（x2+y2+z2）≥（1x+2y+2z）2求出x+2y+2z的最大值，再解关于a的绝对值不等式即可．

    解：由柯西不等式9=（12+22+22）（x2+y2+z2）≥（1x+2y+2z）2

    即x+2y+2z≤3，当且仅当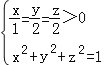

    即，，时，x+2y+2z取得最大值3．

    ∵不等式|a﹣1|≥x+2y+2z，对满足x2+y2+z2=1的一切实数x，y，z恒成立，

    只需|a﹣1|≥3，解得a﹣1≥3或a﹣1≤﹣3，∴a≥4或∴a≤﹣2．

    即实数的取值范围是（﹣∞，﹣2]∪[4，+∞）．

    故答案为：a≥4或a≤﹣2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了解人们对“年月在北京召开的第十三届全国人民代表大会第二次会议和政协第十三届全国委员会第二次会议”的关注度，某部门从年龄在岁到岁的人群中随机调查了人，并得到如图所示的年龄频率分布直方图，在这人中关注度非常髙的人数与年龄的统计结果如表所示：

    年龄

    关注度非常高的人数

    （1）由频率分布直方图，估计这人年龄的中位数和平均数；

    （2）根据以上统计数据填写下面的列联表，据此表，能否在犯错误的概率不超过的前提下，认为以岁为分界点的不同人群对“两会”的关注度存在差异？

    （3）按照分层抽样的方法从年龄在岁以下的人中任选六人，再从六人中随机选两人，求两人中恰有一人年龄在岁以下的概率是多少.

    岁以下

    岁以上

    总计

    非常高

    一般

    总计

    参考数据：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某群体的人均通勤时间，是指单日内该群体中成员从居住地到工作地的平均用时．某地上班族中的成员仅以自驾或公交方式通勤．分析显示：当中（）的成员自驾时，自驾群体的人均通勤时间为（单位：分钟），而公交群体的人均通勤时间不受影响，恒为分钟，试根据上述分析结果回答下列问题：

    （1）当在什么范围内时，公交群体的人均通勤时间少于自驾群体的人均通勤时间？

    （2）求该地上班族的人均通勤时间的表达式；讨论的单调性，并说明其实际意义．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某地区2008年至2014年中，每年的居民人均纯收入y（单位：千元）的数据如下表：

    年份

    2008

    2009

    2010

    2011

    2012

    2013

    2014

    年份代号

    1

    2

    3

    4

    5

    6

    7

    人均纯收入

    2.7

    3.6

    3.3

    4.6

    5.4

    5.7

    6.2

    对变量与进行相关性检验，得知与 之间具有线性相关关系．

    （1）求关于的线性回归方程；

    （2）预测该地区2017年的居民人均纯收入．

    附：回归直线的斜率和截距的最小二乘估计公式分别为：，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，直线经过点，其倾斜角为，以原点为极点，以轴为非负半轴为极轴，与坐标系取相同的长度单位，建立极坐标系.设曲线的极坐标方程为.

    （1）若直线与曲线有公共点，求倾斜角的取值范围；

    （2）设为曲线上任意一点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在极坐标系中，直线的极坐标方程为，现以极点为原点，极轴为轴的非负半轴建立平面直角坐标系，曲线的参数方程为（为参数)．

    （1）求直线的直角坐标方程和曲线的普通方程；

    （2）若曲线为曲线关于直线的对称曲线，点分别为曲线、曲线上的动点，点坐标为，求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中.

    （1）函数的图象能否与轴相切?若能，求出实数，若不能，请说明理由；

    （2）讨论函数的单调性.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国是世界上严重缺水的国家，某市为了制定合理的节水方案，对居民用水情况进行调查，通过抽样，获得某年100为居民每人的月均用水量（单位：吨），将数据按照分成9组，制成了如图所示的频率分布直方图.

    （1）求直方图的的值；

    （2）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，说明理由.

    （3）估计居民月用水量的中位数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，点在以为直径的圆上，垂直与圆所在平面，为的垂心.

    （1）求证：平面平面；

    （2）若，求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案