
已知函数![]() 。
。
(Ⅰ)设![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(Ⅱ)若对任意![]() 恒有
恒有![]() ,求
,求![]() 的取值范围。
的取值范围。
(Ⅰ)f(x)在(-∞, -), (,1), (1,+∞)为增函数, f(x)在(-,)为减函数;(Ⅱ)a∈(-∞,2]时,对任意x∈(0,1)恒有f(x)>1。
(Ⅰ)f(x)的定义域为(-∞,1)∪(1,+∞).对f(x)求导数得 f '(x)= e-ax.
(ⅰ)当a=2时, f '(x)= e-2x, f '(x)在(-∞,0), (0,1)和(1,+ ∞)均大于0,
所以f(x)在(-∞,1), (1,+∞).为增函数.
(ⅱ)当0<a<2时, f '(x)>0, f(x)在(-∞,1), (1,+∞)为增函数.
(ⅲ)当a>2时, 0<<1, 令f '(x)=0 ,解得x1= - , x2= .
当x变化时, f '(x)和f(x)的变化情况如下表:
| x | (-∞, -) | (-,) | (,1) | (1,+∞) |
| f '(x) | + | - | + | + |
| f(x) | ↗ | ↘ | ↗ | ↗ |
f(x)在(-∞, -), (,1), (1,+∞)为增函数,
f(x)在(-,)为减函数.
(Ⅱ)(ⅰ)当0<a≤2时, 由(Ⅰ)知: 对任意x∈(0,1)恒有f(x)>f(0)=1.
(ⅱ)当a>2时, 取x0= ∈(0,1),则由(Ⅰ)知 f(x0)<f(0)=1
(ⅲ)当a≤0时, 对任意x∈(0,1),恒有 >1且e-ax≥1,得
f(x)= e-ax≥ >1. 综上当且仅当a∈(-∞,2]时,对任意x∈(0,1)恒有f(x)>1.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源:2010年四川省眉山市高考数学二模试卷(文科)(解析版) 题型:解答题
 .
. 的值域.
的值域.查看答案和解析>>
科目:高中数学 来源:2015届重庆第49中学七校联盟高一上学期期中考试数学试卷(解析版) 题型:解答题
(本小题满分13分)
已知函数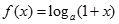 ,
,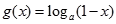 ,
,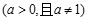 .
.
(Ⅰ)设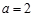 ,函数
,函数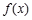 的定义域为
的定义域为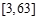 ,求函数
,求函数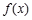 的最值;
的最值;
(Ⅱ)求使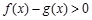 的
的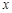 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省高三12月月考理科数学试卷 题型:解答题
已知函数 定义域为
定义域为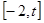 (
(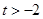 ),设
),设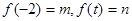 .
.
(1)试确定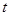 的取值范围,使得函数
的取值范围,使得函数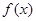 在
在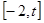 上为单调函数;
上为单调函数;
(2)求证: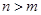 ;
;
(3)求证:对于任意的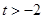 ,总存在
,总存在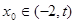 ,满足
,满足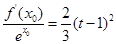 ,并确定这样的
,并确定这样的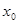 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省南通市高三第二次模拟考试数学试题 题型:填空题
已知函数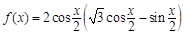 .
.
(1)设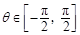 ,且
,且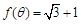 ,求
,求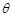 的值;
的值;
(2)在△ABC中,AB=1,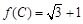 ,且△ABC的面积为
,且△ABC的面积为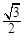 ,求sinA+sinB的值.
,求sinA+sinB的值.
查看答案和解析>>
科目:高中数学 来源:2010年福建省高二下学期期末考试理科数学卷 题型:解答题
(本小题满分12分) 已知函数 .
.
(1) 设F(x)=
 在
在 上单调递增,求
上单调递增,求 的取值范围。
的取值范围。
(2)若函数 与
与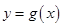 的图象有两个不同的交点M、N,求
的图象有两个不同的交点M、N,求 的取值范围;
的取值范围;
(3)在(2)的条件下,过线段MN的中点作 轴的垂线分别与
轴的垂线分别与 的图像和
的图像和 的图像交S、T点,以S为切点作
的图像交S、T点,以S为切点作 的切线
的切线 ,以T为切点作
,以T为切点作 的切线
的切线 .是否存在实数
.是否存在实数 使得
使得

 ,如果存在,求出
,如果存在,求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com