
分析 不妨设圆的切线为PM,PN,则由$\overrightarrow{PA}$•$\overrightarrow{PB}$≤0,得∠APB≥90°,故∠MPN≥90°,求得PC≤2$\sqrt{2}$,结合题意点E、F到点C的距离等于2$\sqrt{2}$.再利用勾股定理求得EF的最大值.
解答 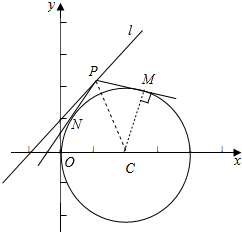 解:由题意,圆心到直线l:y=x+1的距离为$\frac{|2-0+1|}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$>2(半径),故直线l和圆相离.
解:由题意,圆心到直线l:y=x+1的距离为$\frac{|2-0+1|}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$>2(半径),故直线l和圆相离.
从直线上的点向圆上的点连线成角,当且仅当两条线均为切线时,∠APB才是最大的角,
不妨设切线为PM,PN,则由$\overrightarrow{PA}$•$\overrightarrow{PB}$≤0,得∠APB≥90°,∴∠MPN≥90°.
∴sin∠MPC=$\frac{2}{PC}$≥sin45°=$\frac{\sqrt{2}}{2}$,∴PC≤2$\sqrt{2}$.
故在直线l上,当EF最大时,点E、F到点C的距离等于2$\sqrt{2}$.
故EF的长度的最大值为 2$\sqrt{{(2\sqrt{2})}^{2}{-(\frac{3\sqrt{2}}{2})}^{2}}$=2$\sqrt{\frac{7}{2}}$=$\sqrt{14}$,
故答案为:$\sqrt{14}$.
点评 本题主要考查两个向量的数量积的定义,直线和圆的位置关系,勾股定理的应用,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>-1} | B. | {x|-1<x≤1} | C. | {x|-1<x<2} | D. | {x|1<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
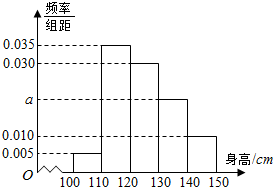 从某小学所有学生中随机抽取100名学生,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),其中样本数据分组[100,110),[110,120),[120,130),[130,140),[140,150),若要从身高在),[120,130),[130,140),[140,150)三组内的学生中,用分层抽样的方法抽取12人参加一项活动,则从身高在[130,140)内的学生中抽取的人数应为4.
从某小学所有学生中随机抽取100名学生,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),其中样本数据分组[100,110),[110,120),[120,130),[130,140),[140,150),若要从身高在),[120,130),[130,140),[140,150)三组内的学生中,用分层抽样的方法抽取12人参加一项活动,则从身高在[130,140)内的学生中抽取的人数应为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com