解:(1)因为函数图象在y轴右边的第一个最高点、最低点的坐标分别是(2,2

)和(10,-2

),
所以A=2

,并且周期T=2(10-2)=16,
所以根据周期公式T=
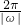
可得ω=

,
所以y=2

sin(

x+φ).
因为函数的一个最高点是(2,2

),并且0<φ<π,
所以φ=

.
所以函数f(x)解析式为
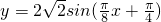
.
(2)将函数y=sinx的图象先向左平移

个单位,得到函数y=sin(x+

)的图象,再将所得图象上所有的点的横坐标变为原来的
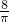
倍(纵坐标不变),最后将所得函数的图象纵坐标伸长为原来的

倍,则所得到的函数图象对应的函数解析式为:y=2

sin(

x+

).
分析:(1)由题意可得:A=2

,并且周期T=16,再根据周期公式可得ω=

,又函数的一个最高点是(2,2

),并且0<φ<π,可得φ=

,进而得到函数的解析式.
(2)将函数y=sinx的图象先向左平移

个单位,再将所得图象上所有的点的横坐标变为原来的
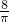
倍,最后将纵坐标伸长为原来的

倍,则可得答案.
点评:本题考查函数y=Asin(ωx+φ)的图象平移变换,在进行平移变换时要注意是先变换ω还是先变换φ,先变换ω与先变换φ的过程是不同的,此题考查学生的逻辑思维能力与推理论证能力,此题是中档题.

 )和(10,-2
)和(10,-2 ).
). )和(10,-2
)和(10,-2 ),
), ,并且周期T=2(10-2)=16,
,并且周期T=2(10-2)=16,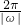 可得ω=
可得ω= ,
, sin(
sin( x+φ).
x+φ). ),并且0<φ<π,
),并且0<φ<π, .
.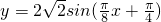 .
. 个单位,得到函数y=sin(x+
个单位,得到函数y=sin(x+ )的图象,再将所得图象上所有的点的横坐标变为原来的
)的图象,再将所得图象上所有的点的横坐标变为原来的 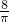 倍(纵坐标不变),最后将所得函数的图象纵坐标伸长为原来的
倍(纵坐标不变),最后将所得函数的图象纵坐标伸长为原来的 倍,则所得到的函数图象对应的函数解析式为:y=2
倍,则所得到的函数图象对应的函数解析式为:y=2 sin(
sin( x+
x+ ).
). ,并且周期T=16,再根据周期公式可得ω=
,并且周期T=16,再根据周期公式可得ω= ,又函数的一个最高点是(2,2
,又函数的一个最高点是(2,2 ),并且0<φ<π,可得φ=
),并且0<φ<π,可得φ= ,进而得到函数的解析式.
,进而得到函数的解析式. 个单位,再将所得图象上所有的点的横坐标变为原来的
个单位,再将所得图象上所有的点的横坐标变为原来的 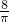 倍,最后将纵坐标伸长为原来的
倍,最后将纵坐标伸长为原来的 倍,则可得答案.
倍,则可得答案.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案 如图,是函数f(x)=Asin(φx+φ)(其中A>0,φ>0,0<φ<π)的部分图象,则其解析为
如图,是函数f(x)=Asin(φx+φ)(其中A>0,φ>0,0<φ<π)的部分图象,则其解析为 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<