
随机抽取某厂的某种产品200件,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而生产1件次品亏损2万元,设一件产品获得的利润为X(单位:万元).
(1)求X的分布列;
(2)求1件产品的平均利润(即X的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.如果此时要求生产1件产品获得的平均利润不小于4.73万元,则三等品率最多是多少?
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为![]() .⑴求
.⑴求![]() 的分布列;⑵求1件产品的平均利润(即
的分布列;⑵求1件产品的平均利润(即![]() 的数学期望);⑶经技术革新后,仍有四个等级的产品,但次品率降为
的数学期望);⑶经技术革新后,仍有四个等级的产品,但次品率降为![]() ,一等品率提高为
,一等品率提高为![]() .如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
查看答案和解析>>
科目:高中数学 来源:2010福建省高二下学期期末考试理科数学卷 题型:解答题
随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为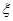 .
.
(1)求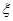 的分布列;
的分布列;
(2)求1件产品的平均利润(即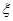 的数学期望);
的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为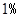 ,一等品率提高为
,一等品率提高为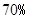 .如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试理科数学(广东卷) 题型:解答题
(本小题满分13分)
随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元。设1件产品的利润(单位:万元)为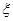 。
。
(1)求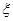 的分布列;
的分布列;
(2)求1件产品的平均利润(即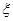 的数学期望);
的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品提高为70%.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com