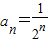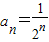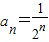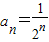若{a
n}为递减数列,则{a
n}的通项公式可以为( )
A.a
n=2n+3
B.a
n=-n
2+3n+1
C.

D.a
n=(-1)
n
【答案】
分析:要判定数列的单调性,根据单调性的定义,考虑利用a
n-a
n-1<0进行检验即可.
解答:解:根据已知可得,a
n-a
n-1<0
A:a
n=2n+3,a
n-a
n-1=2>0,是递增的数列
B:a
n=-n
2+3n+1,a
n-a
n-1=-2n-4,是先增后减
C:
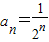
,
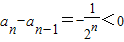
是递减的数列
D:a
n=(-1)
n是摆动数列,不具有单调性
故选C
点评:本题主要考查了利用数列单调性的定义判定数列的单调性,属于基本公式的应用,属于基础试题.
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
若{an}为递减数列,则{an}的通项公式可以为( )
| A、an=2n+3 |
| B、an=-n2+3n+1 |
| C、an= |
| D、an=(-1)n |
查看答案和解析>>
科目:高中数学
来源:2011-2012学年福建师大附中高二(上)期中数学试卷(文科)(解析版)
题型:选择题
若{a
n}为递减数列,则{a
n}的通项公式可以为( )
A.a
n=2n+3
B.a
n=-n
2+3n+1
C.
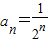
D.a
n=(-1)
n
查看答案和解析>>
科目:高中数学
来源:2012-2013学年福建省泉州市安溪八中高二(上)期中数学试卷(文科)(解析版)
题型:选择题
若{a
n}为递减数列,则{a
n}的通项公式可以为( )
A.a
n=2n+3
B.a
n=-n
2+3n+1
C.
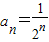
D.a
n=(-1)
n
查看答案和解析>>
科目:高中数学
来源:2011-2012学年福建师大附中高二(上)期中数学试卷(理科)(解析版)
题型:选择题
若{a
n}为递减数列,则{a
n}的通项公式可以为( )
A.a
n=2n+3
B.a
n=-n
2+3n+1
C.
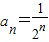
D.a
n=(-1)
n
查看答案和解析>>
科目:高中数学
来源:2010-2011学年湖北省荆州中学高一(下)期中数学试卷(文科)(解析版)
题型:选择题
若{a
n}为递减数列,则{a
n}的通项公式可以为( )
A.a
n=2n+3
B.a
n=-n
2+3n+1
C.
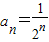
D.a
n=(-1)
n
查看答案和解析>>