
已知 外接圆
外接圆 的半径为
的半径为 ,且
,且 .
.
(Ⅰ)求 边的长及角
边的长及角 的大小;
的大小;
(Ⅱ)从圆 内随机取一个点
内随机取一个点 ,若点
,若点 取自
取自 内的概率恰为
内的概率恰为 ,试判断
,试判断 的形状.
的形状.
(Ⅰ)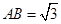 ,
,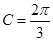 ;(Ⅱ)
;(Ⅱ) 为等边三角形.
为等边三角形.
解析试题分析:(Ⅰ)先利用 的定义结合
的定义结合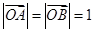 计算出
计算出 的大小,然后在
的大小,然后在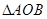 中利用余弦定理即可求出
中利用余弦定理即可求出 边的长,对于角
边的长,对于角 的大小可以根据性质“同弧所对的圆周角是圆心角的一半来计算;(Ⅱ)先利用几何概型计算出
的大小可以根据性质“同弧所对的圆周角是圆心角的一半来计算;(Ⅱ)先利用几何概型计算出 的面积,然后利用三角形的面积公式及余弦定理等求出
的面积,然后利用三角形的面积公式及余弦定理等求出 的三条边
的三条边 、
、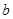 、
、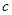 的大小,进而确定
的大小,进而确定 的形状.
的形状.
试题解析:(Ⅰ)依题意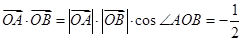 , 2分
, 2分
得 ,又
,又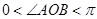 ,故
,故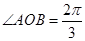 , 4分
, 4分
又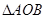 为等腰三角形, 故
为等腰三角形, 故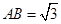 , 5分
, 5分
而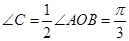 或
或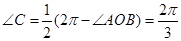 . 6分
. 6分
(Ⅱ)依题意,从圆 内随机取一个点,取自
内随机取一个点,取自 内的概率
内的概率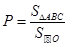 ,
,
可得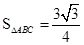 . 8分
. 8分
设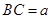 ,
,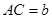 .设
.设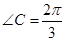 ,由
,由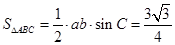 ,得
,得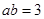 , ①
, ①
由 ,得
,得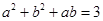 , ②
, ②
联立①②得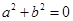 ,这是不可能的. 所以必有
,这是不可能的. 所以必有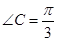 . 9分
. 9分
由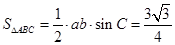 ,得
,得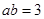 , ①
, ①
由 ,得
,得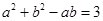 ,
,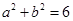 ② 11分
② 11分
联立①② 解得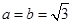 .
.
所以 为等边三角形. 12分
为等边三角形. 12分
考点:平面向量的数量积、圆周角定理、余弦定理、几何概型、三角形的面积公式


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:解答题
在△ABC中,角A,B,C的对边分别为a,b,c.已知2cos(B-C)+1=4cosBcosC.
(Ⅰ)求A;
(Ⅱ)若a=2 ,△ABC的面积为2
,△ABC的面积为2 ,求b+c.
,求b+c.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,有两座建筑物AB和CD都在河的对岸(不知 道它们的高度,且不能到达对岸),某人想测量两 座建筑物尖顶A、C之间的距离,但只有卷尺和测 角仪两种工具.若此人在地面上选一条基线EF,用 卷尺测得EF的长度为a,并用测角仪测量了一些角度: ,
, ,
, ,
, ,
, 请你用文字和公式写出计算A、C之间距离的步骤和结果.
请你用文字和公式写出计算A、C之间距离的步骤和结果.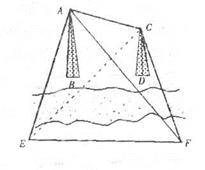
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com