
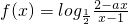 (a是常数).
(a是常数). 可知,
可知, 得:
得: ,或x>1
,或x>1 ;
; 得:
得: ,
,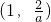 .
. ,
,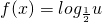 减函数,
减函数, 在(2,4)上是减函数,
在(2,4)上是减函数,

 ]
] ,进而根据常数a<2且a≠0,及分式不等式的解法,分a<0时和0<a<2时两种情况分类讨论,即可得到答案;
,进而根据常数a<2且a≠0,及分式不等式的解法,分a<0时和0<a<2时两种情况分类讨论,即可得到答案; 在(2,4)上是减函数,结合(1)中结论,我们易构造出关于a的不等式组,解不等式组即可得到a的取值范围.
在(2,4)上是减函数,结合(1)中结论,我们易构造出关于a的不等式组,解不等式组即可得到a的取值范围. ,(2)的关键是根据复合函数单调性的确定原则,得到
,(2)的关键是根据复合函数单调性的确定原则,得到 在(2,4)上是减函数,进而构造出关于a的不等式组.本题(2)易忽略对数的真数大于0的同,而错解为0<a<2.
在(2,4)上是减函数,进而构造出关于a的不等式组.本题(2)易忽略对数的真数大于0的同,而错解为0<a<2. 

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源:2012-2013学年安徽省凤阳艺荣高考辅导学校高三(上)第三次月考数学试卷(文科)(解析版) 题型:填空题
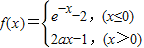 (a是常数且a>0).对于下列命题:
(a是常数且a>0).对于下列命题: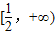 上恒成立,则a的取值范围是a>1;
上恒成立,则a的取值范围是a>1;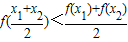 .
.查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省唐山市滦南县司各庄中学高三(上)11月月考数学试卷(解析版) 题型:填空题
 (a是常数且a>0).对于下列命题:
(a是常数且a>0).对于下列命题: 上恒成立,则a的取值范围是a>1;
上恒成立,则a的取值范围是a>1; .
.查看答案和解析>>
科目:高中数学 来源:2011年安徽省淮南市高考数学一模试卷(文科)(解析版) 题型:解答题
 (a是常数且a>0).对于下列命题:
(a是常数且a>0).对于下列命题: 上恒成立,则a的取值范围是a>1;
上恒成立,则a的取值范围是a>1; .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com