

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
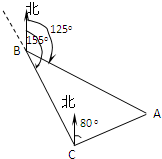 如图,货轮在海上以50浬/时的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为155°的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为125°.半小时后,货轮到达C点处,观测到灯塔A的方位角为80°.求此时货轮与灯塔之间的距离(得数保留最简根号).
如图,货轮在海上以50浬/时的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为155°的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为125°.半小时后,货轮到达C点处,观测到灯塔A的方位角为80°.求此时货轮与灯塔之间的距离(得数保留最简根号).查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,货轮在海上以35n mile/h的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为152°的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为122°.半小时后,货轮到达C点处,观测到灯塔A的方位角为32°.求此时货轮与灯塔之间的距离.
如图,货轮在海上以35n mile/h的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为152°的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为122°.半小时后,货轮到达C点处,观测到灯塔A的方位角为32°.求此时货轮与灯塔之间的距离.查看答案和解析>>
科目:高中数学 来源: 题型:
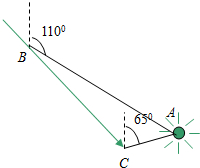 货轮在海上自B点以40km/h的速度沿方向角(从指北方向顺时针转到目标方向线的水平角)为140°的方向航行,为了确定船位,船在B点观测灯塔A的方位角为110°,航行半小时后,船到达C点,观测灯塔A的方位角是65°,问货轮到达C点时,与灯塔A的距离.
货轮在海上自B点以40km/h的速度沿方向角(从指北方向顺时针转到目标方向线的水平角)为140°的方向航行,为了确定船位,船在B点观测灯塔A的方位角为110°,航行半小时后,船到达C点,观测灯塔A的方位角是65°,问货轮到达C点时,与灯塔A的距离.查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省福州市平潭县翰英中学高二(上)第一次月考数学试卷(解析版) 题型:解答题
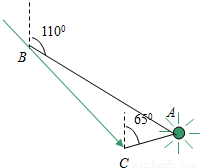
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com