
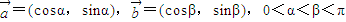
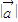 的值;
的值;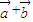 与
与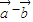 互相垂直;
互相垂直;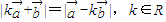 且k≠0,求β-α的值.
且k≠0,求β-α的值.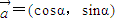 ,能求出
,能求出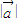 的值.
的值.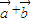 )•(
)•(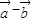 )=(cosα+cosβ)(cosα-cosβ)+(sinα+sinβ)(sinα-sinβ)=0,能证明(
)=(cosα+cosβ)(cosα-cosβ)+(sinα+sinβ)(sinα-sinβ)=0,能证明(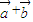 )⊥(
)⊥(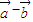 ).
).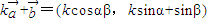 ,
,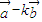 =(cosα-kcosβ,sinα-ksinβ)和|k
=(cosα-kcosβ,sinα-ksinβ)和|k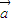 +
+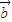 |=|
|=|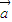 -k
-k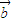 |,能够求出
|,能够求出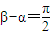 .
.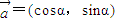 ,
,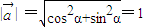 .(3分)
.(3分)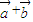 )•(
)•(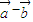 )
)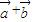 )⊥(
)⊥(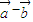 ).(8分)
).(8分)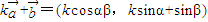 ,
,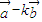 =(cosα-kcosβ,sinα-ksinβ),(10分)
=(cosα-kcosβ,sinα-ksinβ),(10分)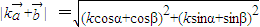
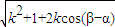 ,(12分)
,(12分)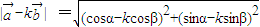
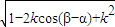 ,
,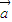 +
+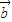 |=|
|=|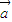 -k
-k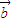 |,
|,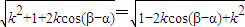 ,
,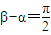 .(14分)
.(14分)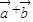 与
与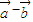 互相垂直和求β-α的值.综合性强,较繁琐,容易出错.解题时要认真审题,注意三角函数恒等变换的灵活运用.
互相垂直和求β-α的值.综合性强,较繁琐,容易出错.解题时要认真审题,注意三角函数恒等变换的灵活运用. 

科目:高中数学 来源:2011年高考试题数学文2(山东卷)解析版 题型:解答题
在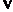 ABC中,内角A,B,C的对边分别为a,b,c.已知
ABC中,内角A,B,C的对边分别为a,b,c.已知 .
.
(I) 求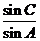 的值;
的值;
(II) 若cosB=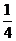 ,
,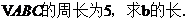
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com