
(1)与![]() 相等的向量是________;
相等的向量是________;
(2)与![]() 长度相等的向量是________;
长度相等的向量是________;
(3)与![]() 共线的向量是________.
共线的向量是________.
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
 已知正方形ABCD的边长为2
已知正方形ABCD的边长为2| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 2 |
A.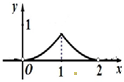 | B.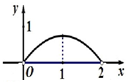 | C.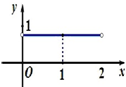 | D.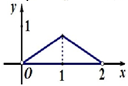 |
查看答案和解析>>
科目:高中数学 来源: 题型:
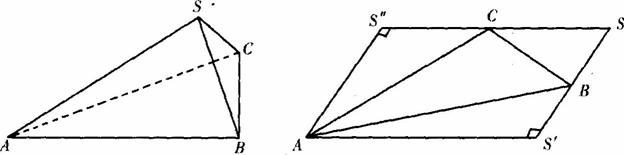
(Ⅰ)求证:顶点S在底面ABC的射影O是底面△ABC的垂心;
(Ⅱ)求SC与底面ABC所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
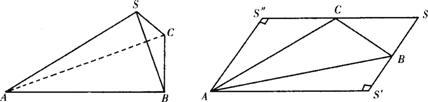
(Ⅰ)求证:顶点S在底面ABC的射影O是底面△ABC的垂心;
(Ⅱ)求SC与底面ABC所成的角的大小.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市朝阳区高三(上)期末数学试卷(理科)(解析版) 题型:选择题
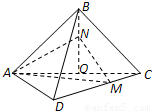 已知正方形ABCD的边长为2
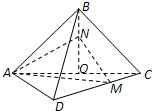
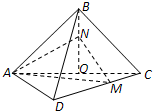
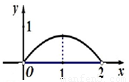
已知正方形ABCD的边长为2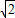 ,将△ABC沿对角线AC折起,使平面ABC⊥平面ACD,得到如图所示的三棱锥B-ACD.若O为AC边的中点,M,N分别为线段DC,BO上的动点(不包括端点),且BN=CM.设BN=x,则三棱锥N-AMC的体积y=f(x)的函数图象大致是( )
,将△ABC沿对角线AC折起,使平面ABC⊥平面ACD,得到如图所示的三棱锥B-ACD.若O为AC边的中点,M,N分别为线段DC,BO上的动点(不包括端点),且BN=CM.设BN=x,则三棱锥N-AMC的体积y=f(x)的函数图象大致是( )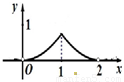
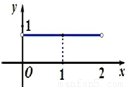
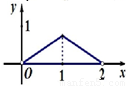
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com