Question

上海电信宽频私人用户月收费标准如下表

方案	类别	基本费用	超时费用
甲	包月制（不限时）	130元	无
乙	有限包月制（限60小时）	80元	3元/小时

假定每月初可以和电信部门约定上网方案
1）某用户每月上网时间为70小时，应选择哪种方案
2）写出方案乙中每月总费用y（元）关于时间t（小时）的函数关系式
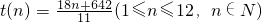3）费先生一年内每月上网时间t（n）（小时）与月份n的函数为，问费先生全年的上网费用最少为多少元？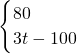

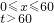Answer 1

解：（1）乙方按月费用为：80+10×3=110元…2分∵110＜130∴应选择乙方案；…3分
（2）y= …7分（写成0＜x＜60不扣分）
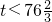（3）由3t-100＜130　得：∴当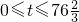时，选择乙方案，当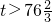时，选甲方案．…9分
即：前11个月选择乙方案，最后一个月选择甲方案．…10分
总费用=[80+3（f（1）-60）]+[80+3（f（2）-60）]+…+[80+3（f（n）-60）+120=1280元…12分
分析：（1）先求出乙方案上网时间为70小时的费用，然后与甲方案的费用进行比较，即可得知选择哪种方案；
（2）乙方案是有限包月制（限60小时），故乙中每月总费用y（元）关于时间t（小时）的函数关系式是以60为分界点的分段函数，低于60小时为常数函数，大于60小时为一次函数，用分段函数表示即可；
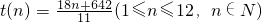（3）先根据甲乙两种方案求出费用相等所需时间，从而得到何时选择哪种方案，再根据函数，为单调递增函数，从而可判定哪些月份选择那种方案，从而求出费先生全年的上网费用最小值．
点评：本题主要考查了函数模型的选择与应用，同时考查了分段函数和等差数列的求和，属于中档题．