
过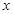 轴上动点
轴上动点 引抛物线
引抛物线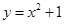 的两条切线
的两条切线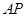 、
、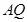 ,
,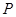 、
、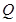 为切点.
为切点.
(1)若切线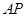 ,
,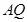 的斜率分别为
的斜率分别为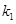 和
和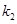 ,求证:
,求证: 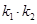 为定值,并求出定值;
为定值,并求出定值;
(2)求证:直线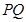 恒过定点,并求出定点坐标;
恒过定点,并求出定点坐标;
(3)当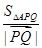 最小时,求
最小时,求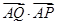 的值.
的值.
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
(09年湖北八校联考文)(13分)过![]() 轴上动点
轴上动点![]() 引抛物线
引抛物线![]() 的两条切线
的两条切线![]() ,
,![]() ,
,![]() ,
,![]() 为切点.
为切点.
(Ⅰ)若切线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() 和
和![]() ,求证:
,求证:![]() 为定值,并求出定值.
为定值,并求出定值.
(Ⅱ) 求证:直线![]() 恒过定点,并求出定点坐标.
恒过定点,并求出定点坐标.
(Ⅲ)当![]() 最小时,求
最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2011年浙江省杭州市高二上学期期末考试数学理卷 题型:解答题
本小题满分14分)
过 轴上动点
轴上动点 引抛物线
引抛物线 的两条切线
的两条切线 、
、 ,
, 、
、 为切点,设切线
为切点,设切线 、
、 的斜率分别为
的斜率分别为 和
和 .
.

(1)求证: ;
;
(2)求证:直线 恒过定点,并求出此定点坐标;
恒过定点,并求出此定点坐标;
(3)设 的面积为
的面积为 ,当
,当 最小时,求
最小时,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2011年浙江省杭州市高二上学期期末考试数学文卷 题型:解答题
(本小题满分14分)
过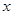 轴上动点
轴上动点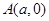 引抛物线
引抛物线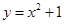 的两条切线
的两条切线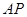 、
、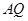 ,
,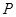 、
、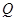 为切点,设切线
为切点,设切线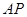 ,
,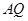 的斜率分别为
的斜率分别为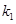 和
和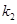 .
.
(1)求证: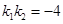 ;
;
(2) 试问:直线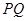 是否经过定点?若是,求出该定点坐标;若不是,请说明理由.
是否经过定点?若是,求出该定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试(重庆卷)数学文史类模拟试卷(二) 题型:解答题
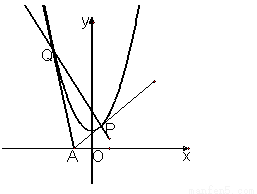
过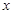 轴上动点
轴上动点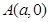 引抛物线
引抛物线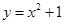 的两条切线
的两条切线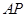 、
、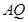 ,
,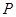 、
、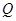 为切点.
为切点.
(Ⅰ)若切线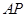 ,
,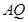 的斜率分别为
的斜率分别为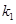 和
和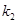 ,求证:
,求证: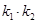 为定值,并求出定值;
为定值,并求出定值;
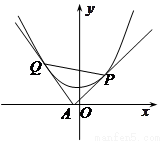 (Ⅱ)求证:直线
(Ⅱ)求证:直线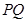 恒过定点,并求出定点坐标;
恒过定点,并求出定点坐标;
(Ⅲ)当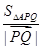 最小时,求
最小时,求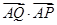 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com