(本小题满分12分)
解:(Ⅰ)∵a=1,b=2,cosC=

,
∴由余弦定理c
2=a
2+b
2-2abcosC得:c
2=1+4-1=4,
解得:c=2,
则△ABC的周长为1+2+2=5;…(6分)
(Ⅱ)∵cosC=

,且C为三角形的内角,
∴sinC=

,
设△ABC的内切圆半径为r,则有S
△ABC=

absinC=

(a+b+c)r,
∴

×1×2×

=

×5×r,
解得:r=
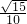
,
又E为AB的中点,
∴S
△CAE=

S
△ABC=
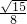
.…(12分)
分析:(Ⅰ)利用余弦定理得到c
2=a
2+b
2-2abcosC,将a,b及cosC的值代入,开方求出c的值,即可得到三角形的周长;
(Ⅱ)由cosC的值,及C为三角形的内角,利用同角三角函数间的基本关系求出sinC的值,设三角形ABC的内切圆半径为r,连接三角形内心与三个顶点,将三角形ABC分为三个高都为r的三角形,可得出三角形的面积等于周长乘以r的一半,表示出三角形的面积,再利用三角形的面积公式表示出三角形的面积,将三角形的周长,a,b及sinC的值代入求出r的值;由E为AB的中点,利用等底同高得到三角形CAE的面积为三角形ABC面积的一半,求出即可.
点评:此题考查了余弦定理,三角形的面积公式,三角形内切圆性质,以及同角三角函数间的基本关系,熟练掌握定理及公式是解本题的关键.

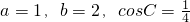 ,E为边AB的中点.
,E为边AB的中点. ,
, ,且C为三角形的内角,
,且C为三角形的内角, ,
, absinC=
absinC= (a+b+c)r,
(a+b+c)r, ×1×2×
×1×2× =
= ×5×r,
×5×r,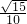 ,
, S△ABC=
S△ABC=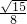 .…(12分)
.…(12分)

 阅读快车系列答案
阅读快车系列答案