
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-4坐标系与参数方程练习卷(解析版) 题型:填空题
设极点与坐标原点重合极轴与x轴正半轴重合,已知直线l的极坐标方程为:ρsin =a,a∈R,圆C的参数方程是
=a,a∈R,圆C的参数方程是 (θ为参数).若圆C关于直线l对称,则a=________.
(θ为参数).若圆C关于直线l对称,则a=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(四)第二章第一节练习卷(解析版) 题型:选择题
函数f(x)=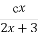 (x≠-
(x≠- )满足f(f(x))=x,则常数c等于( )
)满足f(f(x))=x,则常数c等于( )
(A)3 (B)-3
(C)3或-3 (D)5或-3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(六)第二章第三节练习卷(解析版) 题型:选择题
若偶函数f(x)在(-∞,0)上单调递减,则不等式f(-1)<f(lgx)的解集是( )
(A)(0,10) (B)(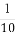 ,10)
,10)
(C)(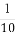 ,+∞) (D)(0,
,+∞) (D)(0,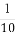 )∪(10,+∞)
)∪(10,+∞)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(八)第二章第五节练习卷(解析版) 题型:解答题
已知函数f(x)=loga(3-ax).
(1)当x∈[0,2]时,函数f(x)恒有意义,求实数a的取值范围.
(2)是否存在这样的实数a,使得函数f(x)在区间[1,2]上为减函数,并且最大值为1?如果存在,试求出a的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(八)第二章第五节练习卷(解析版) 题型:选择题
已知函数f(x)=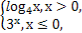 则f(f(
则f(f(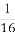 ))=( )
))=( )
(A) (B)-
(B)- (C)9 (D)-9
(C)9 (D)-9
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(五)第二章第二节练习卷(解析版) 题型:解答题
已知f(x)= (x≠a).
(x≠a).
(1)若a=-2,试证f(x)在(-∞,-2)上单调递增.
(2)若a>0且f(x)在(1,+∞)上单调递减,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(三)第一章第三节练习卷(解析版) 题型:选择题
已知命题
p1:函数y=2x-2-x在R上为增函数,
p2:函数y=2x+2-x在R上为减函数,
则在命题q1:p1∨p2,q2:p1∧p2,q3:(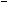 p1)∨p2和q4:p1∧(
p1)∨p2和q4:p1∧(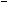 p2)中,真命题是( )
p2)中,真命题是( )
(A)q1,q3 (B)q2,q3 (C)q1,q4 (D)q2,q4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com