
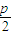 ,0),交抛物线于AB两点,O为坐标原点,那么
,0),交抛物线于AB两点,O为坐标原点,那么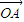 •
•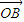 =-
=- p2;
p2;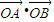 的值;再设出直线方程,把直线与抛物线方程联立,得到A,B两点的坐标和斜率之间的关系,再代入
的值;再设出直线方程,把直线与抛物线方程联立,得到A,B两点的坐标和斜率之间的关系,再代入 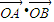 计算即可得到结论.
计算即可得到结论.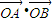 的方法即可得到结论.(注意要分直线斜率存在和不存在两种情况讨论).
的方法即可得到结论.(注意要分直线斜率存在和不存在两种情况讨论).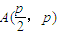 ,
,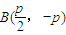 .
.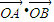 =
=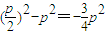 .…(2分)
.…(2分)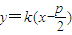 ,A(x1,y1)B(x2,y2).
,A(x1,y1)B(x2,y2).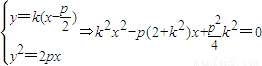
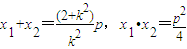 .…(4分)
.…(4分)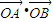 =x1x2+y1y2=
=x1x2+y1y2=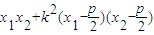 =
=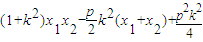 =
=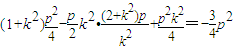 .
.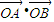 =
=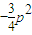 为定值.…(6分)
为定值.…(6分)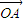 •
•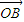 =-
=- p2,那么直线l过抛物线y2=2px (p>0)的焦点F(
p2,那么直线l过抛物线y2=2px (p>0)的焦点F(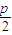 ,0).其为真,
,0).其为真,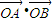 =
= .则
.则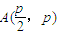 ,
,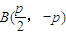
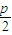 ,0).…(4分)
,0).…(4分)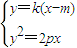 及
及 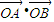 =
=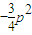 得出m=
得出m= p.
p.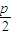 ,0).…(8分)
,0).…(8分)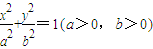 的一个焦点F的动直线l交椭圆于A、B两点,存在定点P,使
的一个焦点F的动直线l交椭圆于A、B两点,存在定点P,使 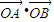 为定值.
为定值.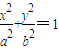 的右焦点F(c,0)(其中
的右焦点F(c,0)(其中  )
)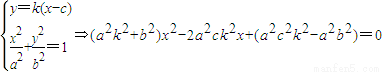 得:
得: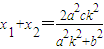 ,
,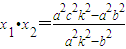 .…(9分)
.…(9分)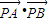 =(x1-m)(x2-m)+y1y2
=(x1-m)(x2-m)+y1y2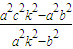 -(m+ck2)
-(m+ck2) 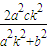 +m2+c2k2
+m2+c2k2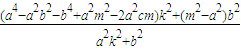
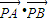 为定值,
为定值,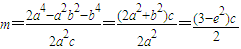
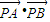 =m2-a2=
=m2-a2=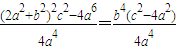 …(12分)
…(12分)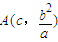 ,
,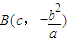 .
.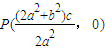
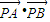 =
=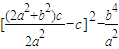 =
=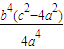 .…(13分)
.…(13分)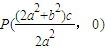
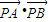 =
=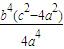 .为定值.…(14分)
.为定值.…(14分)

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
| x2 |
| 16 |
| y2 |
| 9 |
| 5 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 16 |
| y2 |
| 9 |
| 3 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| y2 |
| a2 |
| x2 |
| b2 |
| 2 |
| RM |
| MT |
| RN |
| NT |
查看答案和解析>>
科目:高中数学 来源: 题型:
| p |
| 2 |
| OA |
| OB |
| 3 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com