
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:044
己知数列{An}中,A1>-1,对任意自然数n,都有An+1=![]() .
.
(1) 设A1=1,求A2,A3,A4;
(2)
试比较An与![]() 的大小,并证明你的结论;
的大小,并证明你的结论;
(3)
当A1≠![]() 时,证明:对于任意自然数n,或者都满足A2n-1<A2n+1;或者都满足A2n-1<A2n+1。
时,证明:对于任意自然数n,或者都满足A2n-1<A2n+1;或者都满足A2n-1<A2n+1。
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
(1) 设A1=1,求A2,A3,A4;
(2)
试比较An与![]() 的大小,并证明你的结论;
的大小,并证明你的结论;
(3)
当A1≠![]() 时,证明:对于任意自然数n,或者都满足A2n-1<A2n+1;或者都满足A2n-1<A2n+1。
时,证明:对于任意自然数n,或者都满足A2n-1<A2n+1;或者都满足A2n-1<A2n+1。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年天津市红桥区高二(下)期末数学试卷(理科)(解析版) 题型:填空题
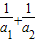 ≥4:若a1,a2,a3∈R+,且a1+a2+a3=1,则
≥4:若a1,a2,a3∈R+,且a1+a2+a3=1,则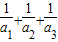 ≥9”,请猜想若a1,a2…an∈R+,且a1+a2+…an=1,则
≥9”,请猜想若a1,a2…an∈R+,且a1+a2+…an=1,则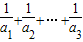 ≥ .
≥ .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com