Question

过点(0,1)的直线与x²＋y²＝4相交于A、B两点，则|AB|的最小值为________．

 

Answer 1

【答案】

2

【解析】

试题分析：要求解直线与圆相交时的弦长，那么结合图像，要使得|AB|的长度最小，那么就是求解半弦长最小时的情况。利用圆的半径和半弦长和弦心距的关系可知， 半径的平方等于弦心距的平方加上半弦长的平方得到。由于半径由x²＋y²＝4可知为2.只要满足圆心（0,0）到过点（0,1）的直线的距离最大即可，那么即为过点（0,1）且与圆心的连线垂直的直线，如图所示，那么此时的弦心距为1，那么利用上述的勾股定理可知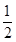|AB|=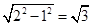，故|AB|的最小值为2，故答案为2。

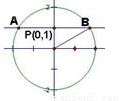
考点：本试题主要是考查了直线与圆的位置关系，计算弦心距，再求半弦长，得出结论．

点评：数形结合解答本题，它是选择题可以口算、心算、甚至不算，得出结果最好．