
设函数 .
.
(1)当 (
(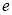 为自然对数的底数)时,求
为自然对数的底数)时,求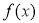 的最小值;
的最小值;
(2)讨论函数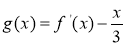 零点的个数;
零点的个数;
(3)若对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1)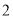 ;(2)当
;(2)当 时,函数
时,函数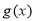 无零点;当
无零点;当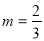 或
或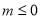 时,函数
时,函数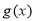 有且只有一个零点;当
有且只有一个零点;当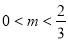 时,函数
时,函数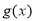 有两个零点;(3)
有两个零点;(3)
【解析】
试题分析:(1)当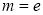 时,
时,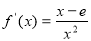 ,令
,令 ,得
,得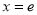 ,将定义域分段并研究导函数
,将定义域分段并研究导函数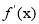 在每段的符号,判断函数大致图象,进而求得最小值;(2)由已知得
在每段的符号,判断函数大致图象,进而求得最小值;(2)由已知得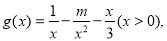 则
则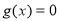 ,进而把问题转化为判断函数图象与
,进而把问题转化为判断函数图象与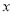 轴交点的个数问题,或者参变分离为
轴交点的个数问题,或者参变分离为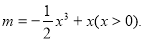 利用导数研究函数
利用导数研究函数 的形状,研究直线
的形状,研究直线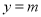 与其交点个数问题即可;(3)通过对不等式恒等变形,研究其蕴含的数学本质,变形为
与其交点个数问题即可;(3)通过对不等式恒等变形,研究其蕴含的数学本质,变形为 ,观察其结构特征,构造函数
,观察其结构特征,构造函数 ,则函数
,则函数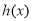 在
在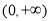 单调递增,转化为
单调递增,转化为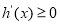 恒成立问题处理.
恒成立问题处理.
试题解析:(1)由题设,当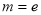 时,
时,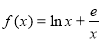 ,则
,则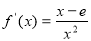 , 1分
, 1分
∴当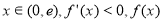 在
在 上单调递减,
上单调递减,
当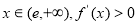 ,
,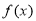 在(
在(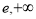 )上单调递增, 2分
)上单调递增, 2分
∴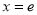 时,
时,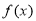 取得极小值
取得极小值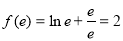
∴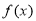 的极小值为2. 3分
的极小值为2. 3分
(2)由题设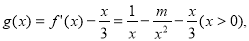
令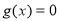 ,得
,得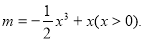 4分
4分
设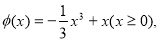
则 5分
5分
当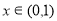 时,
时,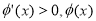 在
在 上单调递增;
上单调递增;
当 时,
时,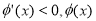 在
在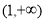 上单调递减。 6分
上单调递减。 6分
∴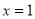 是
是 的唯一极值点,且是极大直点,因此
的唯一极值点,且是极大直点,因此 也是
也是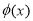 的最大值点,
的最大值点,
∴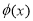 的最大值为
的最大值为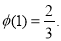 7分
7分
又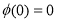 ,结合
,结合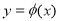 的图像,可知
的图像,可知
①当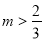 时,函数
时,函数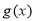 无零点;
无零点;
②当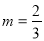 时,函数
时,函数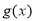 有且只有一个零点;
有且只有一个零点;
③当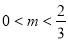 时,函数
时,函数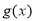 有两个零点;
有两个零点;
④当 时,函数
时,函数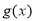 有且只有一个零点。 8分
有且只有一个零点。 8分
综上所述,当 时,函数
时,函数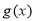 无零点;
无零点;
当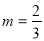 或
或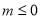 时,函数
时,函数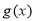 有且只有一个零点;
有且只有一个零点;
当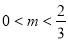 时,函数
时,函数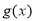 有两个零点; 9分
有两个零点; 9分
(3)对任意的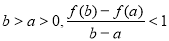 恒成立,
恒成立,
等价于 恒成立(*) 10分
恒成立(*) 10分
设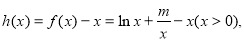
∴(*)等价于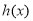 在
在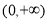 上单调递减. 11分
上单调递减. 11分
由 在
在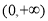 恒成立. 12分
恒成立. 12分
得 恒成立, 13分
恒成立, 13分
∴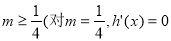 仅在
仅在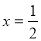 时成立),
时成立),
∴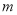 的取值范围是
的取值范围是 14分
14分
考点:1、利用导数求函数的最值、极值;2、函数的零点;3、利用导数研究函数的单调性.


科目:高中数学 来源:2015届河北省石家庄市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
若i为虚数单位,复数z=2﹣i,则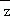 +
+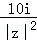 =( ).
=( ).
A.2+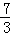 i B.2+i C.2+
i B.2+i C.2+ i D.2+3i
i D.2+3i
查看答案和解析>>
科目:高中数学 来源:2015届河北省石家庄市五校联合体高三上学期第一次月考文科数学试卷(解析版) 题型:选择题
已知实数x,y满足 ,则z=4x+y的最大值为( )
,则z=4x+y的最大值为( )
A.10 B.8 C.2 D.0
查看答案和解析>>
科目:高中数学 来源:2015届河北省唐山市高三10月月考理科数学试卷(解析版) 题型:选择题
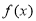 是
是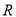 上的偶函数,若将
上的偶函数,若将 的图象向右平移一个单位后,则得到一个奇函数的图象,且
的图象向右平移一个单位后,则得到一个奇函数的图象,且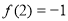 ,则
,则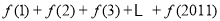 的值为( )
的值为( )
A.-1 B.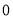 C.1 D.不能确定
C.1 D.不能确定
查看答案和解析>>
科目:高中数学 来源:2015届河北省唐山市高三10月月考理科数学试卷(解析版) 题型:选择题
已知条件 ,条件
,条件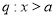 ,若p是q的充分不必要条件,则a的取值范围为( )
,若p是q的充分不必要条件,则a的取值范围为( )
A.a>3 B.a≥3 C.a<-1 D.a≤-1
查看答案和解析>>
科目:高中数学 来源:2015届江西省红色六校高三第一次联考文科数学试卷(解析版) 题型:解答题
对某校高一年级学生参加社区服务次数统计,随机抽去了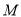 名学生作为样本,得到这
名学生作为样本,得到这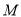 名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下:
名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下:
(1)求出表中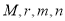 的值;
的值;
(2)在所取样本中,从参加社区服务的次数不少于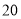 次的学生中任选
次的学生中任选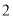 人,求至少一人参加社区服务次数在区间
人,求至少一人参加社区服务次数在区间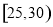 内的概率.
内的概率.
分组 | 频数 | 频率 |
| 9 | 0.45 |
| 5 | n |
| m | r |
| 2 | 0.1 |
合计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源:2015届江西省红色六校高三第一次联考文科数学试卷(解析版) 题型:选择题
设 、
、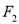 分别为双曲线
分别为双曲线 的左、右焦点.若在双曲线右支上存在点
的左、右焦点.若在双曲线右支上存在点 ,满足
,满足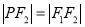 ,且
,且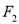 到直线
到直线 的距离等于双曲线的实轴长,则该双曲线的离心率为 ( )
的距离等于双曲线的实轴长,则该双曲线的离心率为 ( )
A. B.2 C.
B.2 C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届江西省南昌市三校高三10月联考理科数学试卷(解析版) 题型:填空题
若函数f(x)=3|cosx|-cosx+m, x∈(0, 2π),有两个互异零点,则实数m的取值范围是_________.
查看答案和解析>>
科目:高中数学 来源:2015届江西省高三上学期第三次考试文科数学试卷(解析版) 题型:填空题
已知 =2
=2 ,
,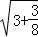 =3
=3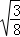 ,
,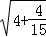 =4
=4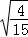 ,…,若
,…,若 =6
=6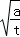 (a,t均为正实数).类比以上等式,可推测a,t的值,则t+a= .2014
(a,t均为正实数).类比以上等式,可推测a,t的值,则t+a= .2014
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com