
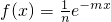 的图象在
的图象在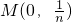 处的切线l与圆C:x2+y2=1相交,则点P(m,n)与圆C的位置关系是
处的切线l与圆C:x2+y2=1相交,则点P(m,n)与圆C的位置关系是 e-m×0=-
e-m×0=- ,∴切线l的方程为mx+ny=1,
,∴切线l的方程为mx+ny=1,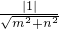 =
= =r,解得
=r,解得 >1
>1 >1,所以点在圆外.
>1,所以点在圆外.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案科目:高中数学 来源:2011届福建省莆田十中高三5月月考调理科数学 题型:解答题
本小题满分14分)
三次函数 的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.
的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.
(1)若函数f(x)为奇函数且过点(1,-3),当x<0时求 的最大值 ;
的最大值 ;
(2)若函数在x=1处取得极值-2,试用c表示a和b,并求 的单调递减区间;
的单调递减区间;
(3)设点A、B、C、D的横坐标分别为 ,
, ,
, ,
,
求证 ;
;
查看答案和解析>>
科目:高中数学 来源:2011-2012学年内蒙古呼伦贝尔市高三第三次模拟考试理科数学试卷 题型:解答题
(本小题满分12分)三次函数 的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.
的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.
(1)若函数f(x)为奇函数且过点(1,-3),当x<0时求 的最大值 ;
的最大值 ;
(2)若函数在x=1处取得极值-2,试用c表示a和b,并求 的单调递减区间;
的单调递减区间;
(3)设点A、B、C、D的横坐标分别为 ,
, ,
, ,
, 求证
求证  ;
;

查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三5月月考调理科数学 题型:解答题
本小题满分14分)
三次函数 的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.
的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.

(1)若函数f(x)为奇函数且过点(1,-3),当x<0时求 的最大值 ;
的最大值 ;
(2)若函数在x=1处取得极值-2,试用c表示a和b,并求 的单调递减区间;
的单调递减区间;
(3)设点A、B、C、D的横坐标分别为 ,
, ,
, ,
,
求证 ;
;
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省宁波市高三(下)4月月考数学试卷(理科)(解析版) 题型:解答题
 x3-x2-3x,g(x)=ax2-3x+b,(a,b∈R,且a≠0,b≠0).满足f(x)与g(x)的图象在x=x处有相同的切线l.
x3-x2-3x,g(x)=ax2-3x+b,(a,b∈R,且a≠0,b≠0).满足f(x)与g(x)的图象在x=x处有相同的切线l. ,求切线l的方程;
,求切线l的方程;查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省宁波市高三(下)4月月考数学试卷(文科)(解析版) 题型:解答题
 x3-x2-3x,g(x)=ax2-3x+b,(a,b∈R,且a≠0,b≠0).满足f(x)与g(x)的图象在x=x处有相同的切线l.
x3-x2-3x,g(x)=ax2-3x+b,(a,b∈R,且a≠0,b≠0).满足f(x)与g(x)的图象在x=x处有相同的切线l. ,求切线l的方程;
,求切线l的方程;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com