
(满分12分)已知点Pn(an,bn)满足an+1=an·bn+1,bn+1= (n∈N*)且点P1的坐标为(1,-1).(1)求过点P1,P2的直线l的方程;
(n∈N*)且点P1的坐标为(1,-1).(1)求过点P1,P2的直线l的方程;
(2)试用数学归纳法证明:对于n∈N*,点Pn都在(1)中的直线l上.
(1)直线l的方程为2x+y=1. (2)见解析。
【解析】
试题分析:(1)由P1的坐标为(1,-1)知a1=1,b1=-1.
∴b2=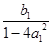 =
=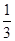 .
a2=a1·b2=
.
a2=a1·b2=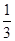 .
.
∴点P2的坐标为(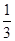 ,
,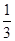 )
)
∴直线l的方程为2x+y=1. …………….3分
(2)①当n=1时,2a1+b1=2×1+(-1)=1成立.…………….4分
②假设n=k(k∈N*,k≥1)时,2ak+bk=1成立,…………….6分
则2ak+1+bk+1=2ak·bk+1+bk+1=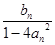 (2ak+1)…………….8分
(2ak+1)…………….8分
=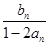 =
=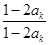 =1,
=1,
∴当n=k+1时,命题也成立. ……………. 10分
由①②知,对n∈N*,都有2an+bn=1,
即点Pn在直线l上. …………….12分
考点:本题主要考查数列的递推公式,数学归纳法,直线方程。
点评:本题将数列问题、直线方程、数学归纳法有机结合在一起,不偏不怪,是一道不错的题目。


科目:高中数学 来源: 题型:
. (本小题满分12分)
已知点![]() 和直线
和直线![]() ,作
,作![]() 垂足为Q,且
垂足为Q,且![]()
(Ⅰ)求点P的轨迹方程;
(Ⅱ)过点C的直线m与点P的轨迹交于两点![]()
![]() 点
点![]() ,若
,若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方
的方![]() 程.
程.
查看答案和解析>>
科目:高中数学 来源:2011届山东省济宁市一中高三年级第二次质量检测数学理卷 题型:解答题
(本小题满分12分)
已知点 在直线
在直线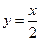 上,其中
上,其中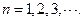
(1)若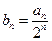 ,求证:数列
,求证:数列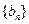 是等差数列;
是等差数列;
(2)若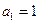 ,求数列
,求数列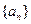 的前
的前 项和
项和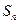 。
。
查看答案和解析>>
科目:高中数学 来源:2011年浙江省苍南县三校高二上学期期中考试数学理卷 题型:解答题
(本小题满分12分)
已知点 及圆
及圆 :
: .
.
(1)若直线 过点
过点 且与圆心
且与圆心 的距离为1,求直线
的距离为1,求直线 的方程;
的方程;
(2)设过点P的直线 与圆
与圆 交于
交于 、
、 两点,当
两点,当 时,求以线段
时,求以线段 为直径的圆
为直径的圆 的方程;
的方程;
 (3)设直线
(3)设直线 与圆
与圆 交于
交于 ,
, 两点,是否存在实数
两点,是否存在实数 ,使得过点
,使得过点 的直线
的直线 垂直平分弦
垂直平分弦 ?若存在,求出实数
?若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010年浙江省高一第二学期期中考试数学试题 题型:解答题
(本小题满分12分)
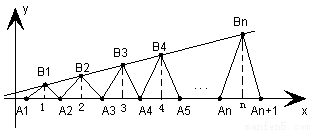
已知点列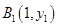 、
、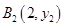 、…、
、…、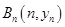 (n∈N)顺次为一次函数
(n∈N)顺次为一次函数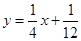 图像上的点,点列
图像上的点,点列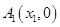 、
、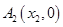 、…、
、…、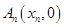 (n∈N)顺次为x轴正半轴上的点,其中
(n∈N)顺次为x轴正半轴上的点,其中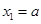 (0<a<1),对于任意n∈N,点
(0<a<1),对于任意n∈N,点 、
、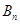 、
、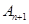 构成一个顶角的顶点为
构成一个顶角的顶点为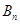 的等腰三角形。
的等腰三角形。
(1)数列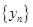 的通项公式,并证明
的通项公式,并证明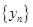 是等差数列;
是等差数列;
(2)证明 为常数,并求出数列
为常数,并求出数列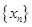 的通项公式;
的通项公式;
(3)上述等腰三角形
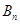
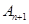 中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。
中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2010年河北省邯郸市高三第二次数学理科试题 题型:解答题
(本小题满分12分)
已知点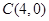 和直线
和直线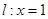 ,作
,作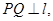 垂足为Q,且
垂足为Q,且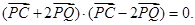
(Ⅰ)求点P的轨迹方程;
(Ⅱ)过点C的直线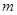 与点P轨迹交于两点
与点P轨迹交于两点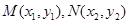 ,
,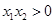 ,点
,点 ,若
,若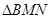 的面积为
的面积为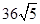 ,求直线
,求直线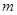 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com