
 方程f(x)=x有唯一的解,已知f(xn)=xn+1(n∈N﹡)且
方程f(x)=x有唯一的解,已知f(xn)=xn+1(n∈N﹡)且
 }是等差数列;
}是等差数列;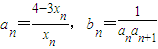 ,求sn=b1+b2+b3+…+bn;
,求sn=b1+b2+b3+…+bn;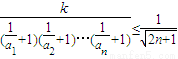 对一切n∈N﹡均成立,求k的最大值.
对一切n∈N﹡均成立,求k的最大值. ,利用f(xn)=xn+1,可得
,利用f(xn)=xn+1,可得 ,取倒数,即可证得数列{
,取倒数,即可证得数列{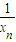 }是等差数列;
}是等差数列;  ,从而可得
,从而可得 ,故
,故 ,由此可求Sn=b1+b2+b3+…+bn.
,由此可求Sn=b1+b2+b3+…+bn. 恒成立,
恒成立, ,则h(n)>0,作商,可得h(n)随n递增,从而可得k的最大值.
,则h(n)>0,作商,可得h(n)随n递增,从而可得k的最大值.


 ,即
,即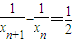
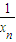 }是等差数列; (4分)
}是等差数列; (4分) ,即
,即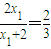 ,解得x1=1
,解得x1=1 ,即
,即
 ,
,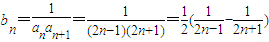
 (1-
(1- +
+ -
- +…+
+…+ )=
)= (8分)
(8分)
 恒成立,
恒成立, ,则h(n)>0
,则h(n)>0
 ,
,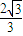 (13分)
(13分)

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 3 |
| 2 |
| A、①②③ | B、②③④ |
| C、①③④ | D、①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 9 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2007•温州一模)设函数y=f(x),我们把满足方程f(x)=0的值x叫做函数y=f(x)的零点.现给出函数f(x)=x3-3x2+ax+a2-10,若它是R上的单调函数,且1是它的零点.
(2007•温州一模)设函数y=f(x),我们把满足方程f(x)=0的值x叫做函数y=f(x)的零点.现给出函数f(x)=x3-3x2+ax+a2-10,若它是R上的单调函数,且1是它的零点.查看答案和解析>>
科目:高中数学 来源:安徽省模拟题 题型:解答题
 方程f(x)=x有唯一的解,已知f(xn)=xn+1(n∈N﹡)且
方程f(x)=x有唯一的解,已知f(xn)=xn+1(n∈N﹡)且
 }是等差数列;
}是等差数列;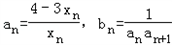 ,求sn=b1+b2+b3+…+bn;
,求sn=b1+b2+b3+…+bn; 对一切n∈N﹡均成立,求k的最大值.
对一切n∈N﹡均成立,求k的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com