
【题目】甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判.每局比赛结束时,负的一方在下局当裁判,假设每局比赛中,甲胜乙的概率为 ![]() ,甲胜丙、乙胜丙的概率都是
,甲胜丙、乙胜丙的概率都是 ![]() ,各局比赛的结果相互独立,第一局甲当裁判.
,各局比赛的结果相互独立,第一局甲当裁判.
(1)求第3局甲当裁判的概率;
(2)记前4局中乙当裁判的次数为X,求X的分布列和数学期望.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)的导函数为f'(x),且满足 ![]() ,f(1)=e,则x>0时,f(x)( )
,f(1)=e,则x>0时,f(x)( )
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值又有极小值
D.既无极大值也无极小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,体现了古代劳动人民的数学智慧,其中第六章“均输”中,有一竹节容量问题,某人根据这一思想,设计了如图所示的程序框图,若输出m的值为35,则输入的a的值为 . 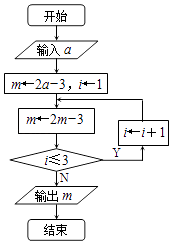
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,已知平面PBC⊥平面ABC.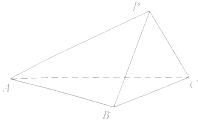
(1)若AB⊥BC,CP⊥PB,求证:CP⊥PA:
(2)若过点A作直线l⊥平面ABC,求证:l∥平面PBC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,已知平面AA1C1C⊥平面ABCD,且 ![]() ,AD=CD=1.
,AD=CD=1.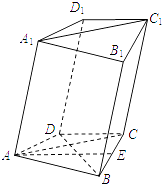
(1)求证:BD⊥AA1;
(2)若E为棱BC的中点,求证:AE∥平面DCC1D1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年5月17日为国际电信日,某市电信公司每年在电信日当天对办理应用套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元.根据以往的统计结果绘出电信日当天参与活动的统计图,现将频率视为概率.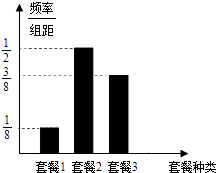
(1)求某两人选择同一套餐的概率;
(2)若用随机变量X表示某两人所获优惠金额的总和,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(2,3)在椭圆 ![]() 上,设A,B,C分别为椭圆的左顶点、上顶点、下顶点,且点C到直线AB的距离为
上,设A,B,C分别为椭圆的左顶点、上顶点、下顶点,且点C到直线AB的距离为 ![]() .
.
(I)求椭圆C的方程;
(II)设M(x1 , y1),N(x2 , y2)(x1≠x2)为椭圆上的两点,且满足 ![]()
![]() =
= ![]() ,求证:△MON的面积为定值,并求出这个定值.
,求证:△MON的面积为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知点P(1,﹣2),直线l: ![]() (m 为参数),以坐标原点为极点,以 x轴的正半轴为极轴建立极坐标系;曲线C的极坐标方程为ρsin2θ=3cosθ;直线l与曲线C的交点为A,B.
(m 为参数),以坐标原点为极点,以 x轴的正半轴为极轴建立极坐标系;曲线C的极坐标方程为ρsin2θ=3cosθ;直线l与曲线C的交点为A,B.
(1)求直线l和曲线C的普通方程;
(2)求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com