练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知和是两个非零的已知向量，当的模取最小值时，（1）求t的值；（2）已知与成角，求证与垂直.

    （1）当时，取最小值；（2）同解析。


    解析:

    （1）设与的夹角为，则

            =

    ∴当时，取最小值

    （2）∵与的夹角为，∴，从而

    所以与垂直

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：学习高手必修四数学苏教版 苏教版 题型：013

    下列四个命题：

    ①若两个非零向量共线，则它们的起点和终点共四个点在同一条直线上；

    ②若两个向量不相等，则它们的终点不可能是同一点；

    ③与已知非零向量共线的单位向量是唯一的；

    ④四边形ABCD是平行四边形的充要条件是与、与分别是共线向量．

    其中正确命题的个数是

    [　　]
    A．

    1

    B．

    2

    C．

    3

    D．

    4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知集合MD是满足下列性质的函数f（x）的全体：存在非零常数k，使得对定义域D内的任意两个不同的实数x1，x2，均有|f（x1）-f（x2）|≤k|x1-x2|成立．
    （Ⅰ） 当D=R时，f（x）=x是否属于MD？说明理由；
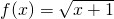    （Ⅱ） 当D=[0，+∞）时，函数数学公式属于MD，求k的取值范围；
    （Ⅲ） 现有函数f（x）=sinx，是否存在函数g（x）=kx+b（k≠0），使得下列条件同时成立：
    ①函数g（x）∈MD；
    ②方程g（x）=0的根t也是方程f（x）=0的根，且g（f（t））=f（g（t））；
    ③方程f（g（x））=g（f（x））在区间[0，2π）上有且仅有一解．若存在，求出满足条件的k和b；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本题满分12分）已知和是两个非零的已知向量，当的模取最小

    值时，（1）求t的值；（2）已知与成角，求证与垂直.

    查看答案和解析>>

    科目：高中数学 来源：2007年江苏省苏州市木渎高级中学高考数学模拟试卷（解析版） 题型：解答题

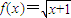    已知集合MD是满足下列性质的函数f（x）的全体：存在非零常数k，使得对定义域D内的任意两个不同的实数x1，x2，均有|f（x1）-f（x2）|≤k|x1-x2|成立．
    （Ⅰ） 当D=R时，f（x）=x是否属于MD？说明理由；
    （Ⅱ） 当D=[0，+∞）时，函数属于MD，求k的取值范围；
    （Ⅲ） 现有函数f（x）=sinx，是否存在函数g（x）=kx+b（k≠0），使得下列条件同时成立：
    ①函数g（x）∈MD；
    ②方程g（x）=0的根t也是方程f（x）=0的根，且g（f（t））=f（g（t））；
    ③方程f（g（x））=g（f（x））在区间[0，2π）上有且仅有一解．若存在，求出满足条件的k和b；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案