
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD.则在三棱锥A-BCD中,下列命题正确的是( ).

A.平面ABD⊥平面ABC
B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC
D.平面ADC⊥平面ABC
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-2练习卷(解析版) 题型:解答题
一个盒子里装有7张卡片,其中有红色卡片4张,编号分别为1,2,3,4;白色卡片3张,编号分别为2,3,4.从盒子中任取4张卡片(假设取到任何一张卡片的可能性相同).
(1)求取出的4张卡片中,含有编号为3的卡片的概率;
(2)在取出的4张卡片中,红色卡片编号的最大值设为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-2练习卷(解析版) 题型:选择题
已知中心在原点的双曲线C的右焦点为F(3,0),离心率等于 ,则C的方程是( ).
,则C的方程是( ).
A. =1 B.
=1 B. =1
=1
C.  =1 D.
=1 D.  =1
=1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(解析版) 题型:填空题
在正方体ABCD-A1B1C1D1中,M,N分别是棱CD,CC1的中点,则异面直线A1M与DN所成的角的大小是________

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(解析版) 题型:解答题
在直角梯形ABCD中,AB∥CD,AD⊥AB,CD=2AB=4,AD= ,E为CD的中点,将△BCE沿BE折起,使得CO⊥DE,其中垂足O在线段DE内.
,E为CD的中点,将△BCE沿BE折起,使得CO⊥DE,其中垂足O在线段DE内.

(1)求证:CO⊥平面ABED;
(2)问∠CEO(记为θ)多大时,三棱锥C-AOE的体积最大,最大值为多少.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-1练习卷(解析版) 题型:解答题
如图是某三棱柱被削去一个底面后的直观图与侧(左)视图、俯视图.已知CF=2AD,侧(左)视图是边长为2的等边三角形;俯视图是直角梯形,有关数据如图所示.求该几何体的体积.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-1练习卷(解析版) 题型:选择题
已知矩形ABCD的面积为8,当矩形ABCD周长最小时,沿对角线AC把
△ACD折起,则三棱锥D-ABC外接的球表面积等于( ).
A.8π B.16π C.48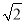 π D.不确定的实数
π D.不确定的实数
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-1练习卷(解析版) 题型:解答题
设{an}是公比不为1的等比数列,其前n项和为Sn,且a5,a3,a4成等差数列.
(1)求数列{an}的公比;
(2)证明:对任意k∈N*,Sk+2,Sk,Sk+1成等差数列.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(解析版) 题型:解答题
某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式y= +10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
+10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求a的值;
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com