
分析 (1)根据平行四边形ABCD中,$\overrightarrow{AD}$=$\overrightarrow{BC}$;列出方程组求出点D的坐标;
(2)根据平面向量数量积的定义求出向量$\overrightarrow{AB}$与$\overrightarrow{BD}$夹角的余弦值.
解答 解:(1)平行四边形ABCD中,A(1,0),B(3,2),C(4,-1);
设D的坐标为(x,y),
则$\overrightarrow{AD}$=$\overrightarrow{BC}$;
即(x-1,y)=(1,-3),
∴$\left\{\begin{array}{l}{x-1=1}\\{y=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$,
∴D(2,-3);
(2)∵$\overrightarrow{AB}$=(2,2),$\overrightarrow{BD}$=(-1,-5),
$\overrightarrow{AB}$•$\overrightarrow{BD}$=2×(-1)+2×(-5)=-12,
|$\overrightarrow{AB}$|=$\sqrt{{2}^{2}{+2}^{2}}$=2$\sqrt{2}$,
|$\overrightarrow{BD}$|=$\sqrt{{(-1)}^{2}{+(-5)}^{2}}$=$\sqrt{26}$,
设$\overrightarrow{AB}$与$\overrightarrow{BD}$的夹角为θ,
则cosθ=$\frac{\overrightarrow{AB}•\overrightarrow{BD}}{|\overrightarrow{AB}|×|\overrightarrow{BD}|}$=$\frac{-12}{2\sqrt{2}×\sqrt{26}}$=-$\frac{3\sqrt{13}}{13}$.
点评 本题考查了平面向量数量积的定义与夹角的计算问题,是基础题.


科目:高中数学 来源: 题型:解答题
 在平面直角坐标系中,已知两定点$A(-\frac{1}{3}\;,\;0)$和$B({\frac{1}{3}\;,\;0})$,点M是平面内的动点,且$|{\overrightarrow{AB}+\overrightarrow{AM}}|+|{\overrightarrow{BA}+\overrightarrow{BM}}|=4$.
在平面直角坐标系中,已知两定点$A(-\frac{1}{3}\;,\;0)$和$B({\frac{1}{3}\;,\;0})$,点M是平面内的动点,且$|{\overrightarrow{AB}+\overrightarrow{AM}}|+|{\overrightarrow{BA}+\overrightarrow{BM}}|=4$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
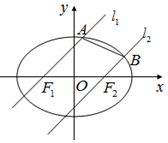 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点分别为F1、F2,离心率为$\frac{1}{2}$,直线y=1与C的两个交点间的距离为$\frac{{4\sqrt{6}}}{3}$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点分别为F1、F2,离心率为$\frac{1}{2}$,直线y=1与C的两个交点间的距离为$\frac{{4\sqrt{6}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 把正偶数数列{2n}的各项从小到大依次排成如图的三角形数阵,记M(r,t)表示该数阵中第r行的第t个数,则数阵中的数2 012对应于第45行的第16个数.
把正偶数数列{2n}的各项从小到大依次排成如图的三角形数阵,记M(r,t)表示该数阵中第r行的第t个数,则数阵中的数2 012对应于第45行的第16个数.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,Rt△ABC的顶点A坐标(-2,0),直角顶点B(0,-2$\sqrt{2}$),顶点C在x轴上,点P为线段OA的中点.
如图所示,Rt△ABC的顶点A坐标(-2,0),直角顶点B(0,-2$\sqrt{2}$),顶点C在x轴上,点P为线段OA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 重合 | C. | 垂直 | D. | 平行 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com