
选修4—4:坐标系与参数方程
在平面直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数).以原点为极点,
为参数).以原点为极点, 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆 的方程为
的方程为 .
.
(Ⅰ)写出直线 的普通方程和圆
的普通方程和圆 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点 的直角坐标为
的直角坐标为 ,圆
,圆 与直线
与直线 交于
交于 两点,求
两点,求 的值.
的值.
科目:高中数学 来源:2017届江苏南通中学高三上期中数学(理)试卷(解析版) 题型:解答题
已知曲线C的极坐标方程为 ?=2cosθ,直线l的极坐标方程为 ? sin(θ+ )=m.若直线l与曲线C有且只有一个公共点,求实数m的值.
)=m.若直线l与曲线C有且只有一个公共点,求实数m的值.
查看答案和解析>>
科目:高中数学 来源:2017届湖北荆荆襄宜四地七校联盟高三理上联考一数学试卷(解析版) 题型:选择题
已知在 内有一点
内有一点 ,满足
,满足 ,过点
,过点 作直线
作直线 分别交
分别交 、
、 于
于 、
、 ,若
,若 ,
, ,则
,则 的最小值为
的最小值为
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2017届广东韶关市六校高三10月联考数学(文)试卷(解析版) 题型:解答题
某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,则每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(Ⅰ)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(Ⅱ)商店记录了50天该商品的日需求量(单位:件),整理得下表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 10 | 15 | 10 | 5 |
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,记“当天的利润在区间 ”为事件A,求P(A)的估计值.
”为事件A,求P(A)的估计值.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年湖北孝感市七校联盟高二理上期中数学试卷(解析版) 题型:填空题
给出一个如图所示的程序框图,若要使输入的 值与输出的
值与输出的 值相等,则这样的
值相等,则这样的 值得个数是个.
值得个数是个.

查看答案和解析>>
科目:高中数学 来源:2017届山东省青州市高三10月段测数学试卷(解析版) 题型:解答题
若二次函数 (
( ,
, ,
, )满足
)满足 ,且
,且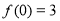 .
.
(1)求 的解析式;
的解析式;
(2)若在区间 上,不等式
上,不等式 恒成立,求实数
恒成立,求实数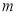 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com