
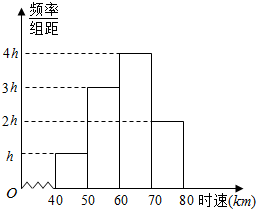
分析 (1)根据频率和为1,列出方程求出h的值,再计算车速在[60,70)的概率;
(2)根据车速的中位数两边直方图的面积相等,求出中位数v的值;
(3)根据频率分布直方图,求出平均车速.
解答 解:(1)因为所有小长方形的面积之和为1,
所以10h+10×3h+10×4h+10×2h=1,
解得h=0.01,
所以车速在[60,70)的概率为10×4h=0.4;
(2)车速的中位数两边直方图的面积相等,于是得:
10×0.01+10×0.03+(v-60)×0.04=0.5,
解得v=62.5(km/h);
(3)根据频率分布直方图,求平均车速为
0.01×10×45+0.03×10×55+0.04×10×65+0.02×10×75=62(km/h).
点评 本题考查了利用频率分布直方图求中位数与平均数的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
| 直径/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
| 件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为:“若方程x2+x-m=0无实根,则m≤0” | |
| B. | 若p∧q为假命题,则p,q均为假命题 | |
| C. | “x=1”是“x2-3x+2=0”的充分不必要条件 | |
| D. | 若椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1的两焦点为F1、F2,且弦AB过F1点,则△ABF2的周长为20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 45°或135° | D. | 60° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆 | B. | 椭圆 | C. | 双曲线的一支 | D. | 直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $sinαcos(α+\frac{π}{6})-cosαsin(α+\frac{π}{6})=-\frac{1}{2}$ | B. | $tan(α+\frac{π}{4})=\frac{1-tanα}{1+tanα}$ | ||
| C. | $sin(α+\frac{π}{4})=sinα+cosα$ | D. | sinαcosα=sinα |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10个 | B. | 9个 | C. | 8个 | D. | 2个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com