设 x=0是函数f(x)=(x2+ax+b)ex(x∈R)的一个极值点.
(1)求 a与b的关系式(用a表示b),并求f(x)的单调区间;
(2)设 a>0,g(x)=-(a2-a+1)ex+2,问是否存在ξ1,ξ2∈[-2,2],使得|f(ξ1)-g(ξ2)|≤1成立?若存在,求 a的取值范围;若不存在,说明理由.
【答案】
分析:(1)先求出其导函数,把x=0直接代入导函数即可求出a与b的关系式b=-a;再求出其导函数f'(x)=[x
2+(a+2)x]e
x=x(x+a+2)e
x,以及导数为0的根0和-a-2,讨论两根的大小即可求出f(x)的单调区间;
(2)先由 a>0求出f(x)与g(x)在[-2,2]上的单调性以及值域,再利用在[-2,2]上,f
min(x)-g
max(x)=-a+(a
2-a+1)=(a-1)
2≥0,即可得a所满足的不等式,解不等式即可求a的取值范围.
解答:解:(1)f'(x)=[x
2+(a+2)x+a+b]e
x(2分)
由f'(0)=0,得b=-a(4分)
∴f(x)=(x
2+ax-a)e
xf'(x)=[x
2+(a+2)x]e
x=x(x+a+2)e
x.
令f'(x)=0,得x
1=0,x
2=-a-2
由于x=0是f(x)极值点,故x
1≠x
2,即a≠-2
当a<-2时,x
1<x
2,故f(x)的单调增区间是(-∞,0]和[-a-2,+∞),单调减区间是[0,-a-2](6分)
当a>-2时,x
1>x
2,故f(x)的单调增区间是(-∞,-a-2]和[0,+∞),单调减区间是[-a-2,0](8分)
(2)当a>0时,-a-2<-2,f(x)在[-2,0]上单调递减,在[0,2]上单调递增,
因此f(x)在[-2,2]上的值域为[f(0),max[f(-2),f(2)]]=[-a,(4+a)e
2](10分)
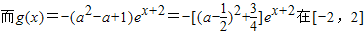
上单调递减,
所以值域是[-(a
2-a+1)]e
4,-(a
2-a+1)](12分)
因为在[-2,2]上,f
min(x)-g
max(x)=-a+(a
2-a+1)=(a-1)
2≥0(13分)
所以,a只须满足
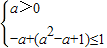
,解得0<a≤2
即当a∈(0,2]时,存在ξ
1、ξ
2∈[-2,2]使得|f(ξ
1)-g(ξ
2)|≤1成立.(14分)
点评:本题主要考查利用导数研究函数的极值以及利用导数研究函数的单调性.在利用导数研究函数的单调性时,导函数为正对应的区间为原函数的增区间;导函数为负对应的区间为原函数的减区间.

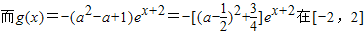 上单调递减,
上单调递减,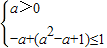 ,解得0<a≤2
,解得0<a≤2

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案