(1)设曲线y=f(x)在点(1,f(1))处的切线为l,若l与圆(x+1)2+y2=1相切,求a的值;?
(2)求函数f(x)的单调区间.
解析:(1)依题意,有x＜2,f′(x)=a+
,?
过(1,f(1))点的直线的斜率为a-1,所以过(1,f(1))点的直线方程为y-a=(a-1)(x-1).?
又已知圆圆心为(-1,0),半径为1,?
依题意,有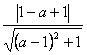
=1.解之,得a=1.?
(2)f′(x)=
=a［x-(2-
)］
,?
当a＞0时,2-
＜2,?
令f′(x)＞0,解得x＜2-
;?
令f′(x)＜0,解得2-
＜x＜2.?
所以(-∞,2-
)是f(x)的增区间;?
(2-
,2)是f(x)的减区间.?
(3)当2-
≤0,即0＜a≤
时,f(x)在［0,1］上是减函数,?
所以f(x)的最小值为f(1)=a.?
当0＜2-
＜1,即
＜a＜1
时,f(x)在(0,2-)上是增函数,在(2-
,1)上是减函数,?
所以需比较f(0)=ln2和f(1)=a两个值的大小.?
因为
＜2＜e,所以
=lne＜ln2＜lne=1.?
所以,当
＜a＜ln2时,最小值为a;当ln2≤a＜1时,最小值为ln2.?
当2-
≥1,即a≥1时,f(x)在［0,1］上是增函数,所以最小值为f(0)=ln2.?
综上,当0＜a＜ln2时,f(x)的最小值为a,当a≥ln2时,f(x)的最小值为ln2.
阅读快车系列答案科目：高中数学 来源： 题型：
(1)当b＞0时,若对任意x∈R都有f(x)≤1,证明a≤
;
(2)当0＜b≤1时,讨论:对任意x∈［0,1］,|f(x)|≤1的充要条件.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年人教版高考数学文科二轮专题复习提分训练15练习卷（解析版） 题型：选择题
已知a>0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
(A)?x∈R,f(x)≤f(x0) (B)?x∈R,f(x)≥f(x0)
(C)?x∈R,f(x)≤f(x0) (D)?x∈R,f(x)≥f(x0)
查看答案和解析>>
科目：高中数学 来源：2010-2011年江西省高二下学期第二次月考数学文卷 题型：选择题
已知a＞0,函数f(x)=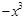 
+ax在［1,+∞)上是减函数，则a的取值范围是(
)
A. a≥1 B. 0＜a≤2 C. 0＜a≤3 D. 1≤a≤3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com