
已知函数 ,其图象在点
,其图象在点 处的切线方程为
处的切线方程为
(1)求 的值;
的值;
(2)求函数 的单调区间,并求出
的单调区间,并求出 在区间[-2,4]上的最大值.
在区间[-2,4]上的最大值.
(1) a=1,b=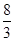 .
(2)8.
.
(2)8.
【解析】
试题分析:(1)f′(x)=x2-2ax+a2-1, 2分
∵(1,f(1))在x+y-3=0上,∴f(1)=2, 3分
∵(1,2)在y=f(x)的图象上,∴2=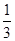 -a+a2-1+b,
-a+a2-1+b,
又f′(1)=-1,∴a2-2a+1=0,
解得a=1,b=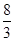 .
6分
.
6分
(2)∵f(x)=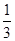 x3-x2+
x3-x2+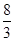 ,∴f′(x)=x2-2x,
,∴f′(x)=x2-2x,
由f′(x)=0可知x=0和x=2是f(x)的极值点,所以有
|
x |
(-∞,0) |
0 |
(0,2) |
2 |
(2,+∞) |
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
? |
极大值 |
? |
极小值 |
? |
8分
所以f(x)的单调递增区间是(-∞,0)和(2,+∞),单调递减区间是(0,2). 10分
∵f(0)=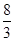 ,f(2)=
,f(2)= ,f(-2)=-4,f(4)=8,
,f(-2)=-4,f(4)=8,
∴在区间[-2,4]上的最大值为8. 13分
考点:导数的几何意义;利用导数研究函数的单调性;利用导数研究函数的最值。
点评:我们要灵活应用导数的几何意义求曲线的切线方程,尤其要注意切点这个特殊点,充分利用切点即在曲线方程上,又在切线方程上,切点处的导数等于切线的斜率这些条件列出方程组求解。属于基础题。


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源:2014届宁夏高二上学期期末考试文科数学试卷(解析版) 题型:解答题
(本题满分12分)
已知函数 ,其图象在点(1,
,其图象在点(1, )处的切线方程为
)处的切线方程为
(1)求a,b的值;
(2)求函数 的单调区间,并求出
的单调区间,并求出 在区间[—2,4]上的最大值。
在区间[—2,4]上的最大值。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省高三第三次考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数 ,其图象在点
,其图象在点 处的切线方程为
处的切线方程为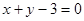 .
.
(1)求 的值;
的值;
(2)求函数 的单调区间,并求出
的单调区间,并求出 在区间
在区间 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中数学 来源:2010年春高二期末数学试卷(理科)(解析版) 题型:解答题
 ,其图象在点(0,-1)处的切线为l.
,其图象在点(0,-1)处的切线为l.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com