
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
在平面直角坐标系中,定义d(P,Q)=|x1﹣x2|+|y1﹣y2|为两点P(x1,y1),Q(x2,y2)之间的“折线距离”.在这个定义下,给出下列命题:①到原点的“折线距离”等于1的点的集合是一个正方形;
②到原点的“折线距离”等于1的点的集合是一个圆;
③到M(﹣1,0),N(1,0)两点的“折线距离”之和为4的点的集合是面积为6的六边形;
④到M(﹣1,0),N(1,0)两点的“折线距离”差的绝对值为1的点的集合是两条平行线.
其中正确的命题是 .(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
若设函数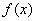 的定义域为D,若存在非零实数
的定义域为D,若存在非零实数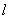 使得对于任意
使得对于任意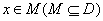 ,有
,有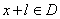 ,且
,且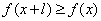 ,则称
,则称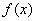 为M上的
为M上的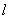 高调函数。如果定义域为R的函数
高调函数。如果定义域为R的函数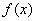 是奇函数,当
是奇函数,当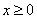 时,
时,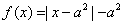 ,且
,且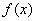 为R上的4高调函数,那么实数
为R上的4高调函数,那么实数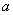 的取值范围是 ( )
的取值范围是 ( )
(A)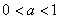 (B)
(B) 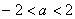 (C)
(C)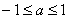 (D)
(D)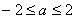
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数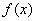 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,在[0,2]上
,在[0,2]上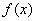 是
是 增函
增函
数,则下 列结论:(1)若
列结论:(1)若 ,则
,则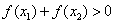 ;
;
(2)若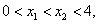 且
且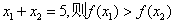 ;
;
(3)若方程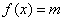 在[-8,8]内恰有四个不同的根
在[-8,8]内恰有四个不同的根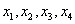 ,则
,则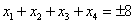 ;
;
其中正确的有( )
A.0个 B.1个 C.2个  D.3个
D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com