
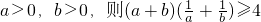 ;
;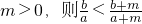 ;
;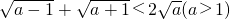 .
. =2+
=2+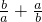
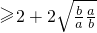 =4,
=4,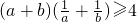 成立;
成立;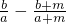 =
=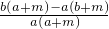 =
=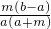 ,∴当a=b时,式子为0,
,∴当a=b时,式子为0,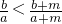 不一定成立;
不一定成立;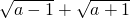 )2-(
)2-(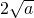 )2=a-1+a+1+
)2=a-1+a+1+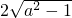 -4a=2(
-4a=2(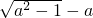 )
)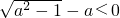 ,因为a2-1-a2=-1<0,故
,因为a2-1-a2=-1<0,故 成立.
成立.

科目:高中数学 来源: 题型:
| x |
| x2+1 |
| 3 |
| 4 |
| 1 |
| 3 |
| 3 |
| 10 |
| 3 |
| 4 |
| a |
| a2+1 |
| b |
| b2+1 |
| c |
| c2+1 |
| 9 |
| 10 |
| n |
 |
| k=1 |
| ak | ||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:013
已知函数f(x)=ax2+bx+c(a>0),α、β为方程f(x)=x的两根,且0<α<β<![]() ,0<x<a,给出下列不等式:
,0<x<a,给出下列不等式:
①x<f(x) ②a<f(x) ③x>f(x) ④a>f(x)
其中成立的是
[ ]
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河北省高三第一次调研考试数学理卷 题型:填空题
下列说法:
①已知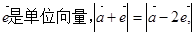 则
则 方向上的投影为
方向上的投影为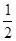 ;
;
②关于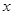 的不等式
的不等式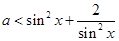 恒成立,则
恒成立,则 的取值范围是
的取值范围是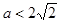 ;
;
③函数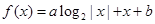 为奇函数的充要条件是
为奇函数的充要条件是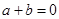 ;
;
④将函数 图像向右平移
图像向右平移 个单位,得到函数
个单位,得到函数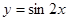 的图像
的图像
其中正确的命题序号是 (填出所有正确命题的序号)。
查看答案和解析>>
科目:高中数学 来源:2009-2010学年江苏省淮安市清江中学高二(上)期末数学试卷(解析版) 题型:解答题
 .
. 时,证明函数y=f(x)图象在点
时,证明函数y=f(x)图象在点 处切线的下方;
处切线的下方; ,且a+b+c=1,证明:
,且a+b+c=1,证明: ”;
”; 的最大值.(只指出正确结论,不要求证明)
的最大值.(只指出正确结论,不要求证明)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com