
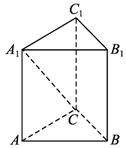
(1)证明三棱柱ABC—A1B1C1是正三棱柱;
(2)若m=![]() n,求直线CA1与平面A1ABB1所成解的大小.
n,求直线CA1与平面A1ABB1所成解的大小.
(1)证明:![]() =
=![]() -
-![]()
=(m,0,0)-(![]() ,-
,-![]() ,0)
,0)
=(![]() ,
,![]() ,0),
,0),
|![]() |=|
|=|![]() |=|
|=|![]() |=m,
|=m,
∴△ABC为正三角形.
又![]() ·
·![]() =0,
=0,![]() ·
·![]() =0,
=0,
∴AA1⊥AB,AA1⊥AC.
又AB∩AC=A,∴AA1⊥平面ABC.
∴三棱术ABC—A1B1C1是正三棱柱.
(2)解:作CD⊥AB于D,连结A1D.

∵AA1⊥平面ABC,∴面AA1B1B⊥平面ABC.
∴CD⊥平面AA1B1B.
因此A1D为斜线A1C在平面AA1B1B上的射影.
∠CA1D为直线CA1与平面AA1B1B所成的角.
在Rt△CDA1中,CD=![]() m,
m,
A1D=![]() =
=![]() .
.
tan∠CA1D=![]() =
=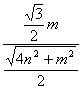 =
=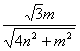 .
.
又m=![]() n,
n,
∴tan∠CA1D=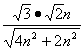 =1.
=1.
又0<∠CA1D<![]() ,
,
∴∠CA1D=45°.


科目:高中数学 来源:2012-2013学年广东高二第二次月考文科数学试卷(解析版) 题型:填空题
已知三棱柱ABC-A´B´C´所有的棱长均为2,且侧棱与底面垂直,则该三棱柱的体积
是
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省云浮市高二(上)12月月考数学试卷(文科)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com