
(1)求椭圆C的方程;
(2)过点A作直线与椭圆C只有一个公共点D,求过B,D两点,且以AD为切线的圆的方程;(6分)
(3)过点A作直线l交椭圆C于P,Q两点,过点P作x轴的垂线交椭圆C于另一点S,若![]() =t
=t![]() (t>1),求证:
(t>1),求证:![]() =t
=t![]() .
.
解:(1)设椭圆的标准方程为![]() +
+![]() =1(a>b>0),依题意得
=1(a>b>0),依题意得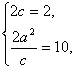 得
得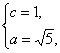 ∴b2=4.
∴b2=4.
∴椭圆的标准方程为![]() +
+![]() =1.
=1.
(2)设过点A的直线方程为y=k(x-5),代入椭圆方程![]() +
+![]() =1得
=1得
(4+5k2)x2-50k2x+125k2-20=0.(*)依题意得Δ=0,即(50k2)2-4(4+5k2)(125k2-20)=0,
得k=±![]() ,且方程的根为x=1,∴D(1,±
,且方程的根为x=1,∴D(1,±![]() ).
).
当点D位于x轴上方时,过点D与AD垂直的直线与x轴交于点E,
直线DE的方程是y-![]() =
=![]() (x-1),∴E(
(x-1),∴E(![]() ,0).
,0).
所求圆即为以线段DE为直径的圆,故方程为(x![]() )2+(y
)2+(y![]() )=
)=![]() .
.
同理可得:当点D位于x轴下方时,圆的方程为(x![]() )2+(y+
)2+(y+![]() )=
)=![]() .
.
(3)设P(x1,y1),Q(x2,y2),由![]() =t
=t![]() 得
得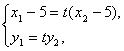 代入
代入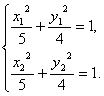
∴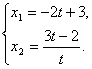 (**)要证
(**)要证![]() =t
=t![]() ,即证
,即证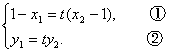
由方程组(**)可知方程组①成立,②显然成立.∴![]() =t
=t![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
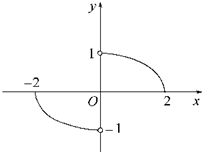 如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{x|-
| ||||||||
B、{x|-2≤x<-
| ||||||||
C、{x|-2≤x<-
| ||||||||
D、{x|-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
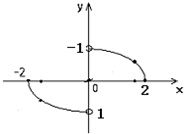 如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{
| ||||||||
B、{x|-2≤x<
| ||||||||
C、{x|-
| ||||||||
D、{x|-
|
查看答案和解析>>
科目:高中数学 来源:2010-2011年山西省孝义市高二第二次月考考试数学文卷 题型:解答题
(12分)
已知椭圆中心在原点,焦点在x轴上,长轴长等于12,离心率为 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过椭圆左顶点作直线l垂直于x轴,若动点M到椭圆右焦点的距离比它到直线l的距离小4,求点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源:东城区模拟 题型:解答题
| ||
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com