
如图 所示,在三棱锥
所示,在三棱锥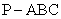 中,
中,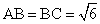 ,平面
,平面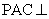 平面
平面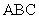 ,
,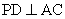 于点
于点 ,
,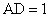 ,
,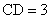 ,
,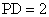 .
.
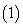 求三棱锥
求三棱锥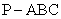 的体积;
的体积;
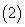 证明:
证明: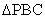 为直角三角形.
为直角三角形.
 |
(1)证明:因为平面 平面
平面 ,平面
,平面 平面
平面 ,
,  平面
平面 ,
, ,所以
,所以 平面
平面 .………………………………………2分
.………………………………………2分
记 边上的中点为
边上的中点为 ,在△
,在△ 中,因为
中,因为 ,
,
所以 .
.
因为 ,
, ,
,
所以 .……………………………………4分
.……………………………………4分
所以△ 的面积
的面积 .……………………………………5分
.……………………………………5分
因为 ,
,
 所以三棱锥
所以三棱锥 的体积
的体积
 .………7分
.………7分
(2)证法1:因为
 ,所以△
,所以△ 为直角三角形.
为直角三角形.
因为 ,
, ,
,
所以 .………9分
.………9分
连接 ,在
,在 △
△ 中,
中,
因为 ,
, ,
, ,
,
所以 .……10分
.……10分
由(1)知 平面
平面 ,又
,又 平面
平面 ,
,
所以
 .
.
在 △
△ 中,因为
中,因为 ,
, ,
, ,
,
所以 .……………………………………12分
.……………………………………12分
在 中,因为
中,因为 ,
, ,
, ,
,
所以 .……………………………………………………………13分
.……………………………………………………………13分
所以 为直角三角形.…………………………………………………………14分
为直角三角形.…………………………………………………………14分
证法2:连接 ,在
,在 △
△ 中,因为
中,因为 ,
, ,
, ,
,
 所以
所以 .…………8分
.…………8分
在△ 中,
中, ,
, ,
, ,
,
所以 ,所以
,所以 .……10分
.……10分
由(1)知 平面
平面 ,
,
因为 平面
平面 ,
,
所以 .
.
因为 ,
,
所以 平面
平面 .………………………………………………………………12分
.………………………………………………………………12分
因为 平面
平面 ,所以
,所以 .
.
所以 为直角三角形.
为直角三角形.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com