
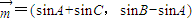 ,
,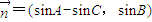 ,且
,且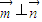 .
. ,试求
,试求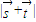 的取值范围.
的取值范围.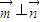 推断出
推断出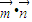 =0,利用向量的基本运算求得sin2C=sin2A+sin2B-sinAsinB,利用正弦定理把角的正弦转化成边,代入余弦定理求得cosC的值,进而求得C.
=0,利用向量的基本运算求得sin2C=sin2A+sin2B-sinAsinB,利用正弦定理把角的正弦转化成边,代入余弦定理求得cosC的值,进而求得C.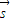 和
和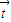 的坐标可求得
的坐标可求得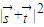 的表达式,然后利用二倍角公式化简整理,利用A的范围和正弦函数的单调性求得
的表达式,然后利用二倍角公式化简整理,利用A的范围和正弦函数的单调性求得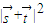 的范围,进而求得
的范围,进而求得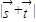 的取值范围.
的取值范围.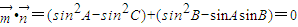
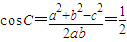
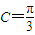
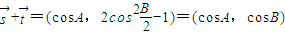
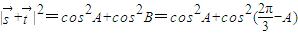
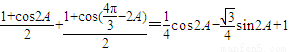
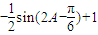
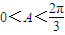 ,∴
,∴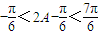
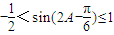
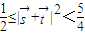 ,故
,故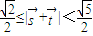 .
.

科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
| s |
| t |
| B |
| 2 |
| s |
| t |
查看答案和解析>>
科目:高中数学 来源:孝感模拟 题型:解答题
| m |
| n |
| m |
| n |
| s |
| t |
| B |
| 2 |
| s |
| t |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省孝感市高三第二次统考数学试卷(理科)(解析版) 题型:解答题
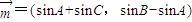 ,
,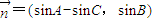 ,且
,且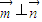 .
. ,试求
,试求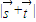 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com